Der kürzeste Flugweg ist sicher die Raumdiagonale, denn einer kürzere als die geradlinige Verbindung zweier Punkte gibt es nicht .
Die Raumdiagonale R hat bei einem Würfel mit der Kantenlänge 0,5 m die Länge
R = √ ( 0,5 2 + 0,5 2 + 0,5 2 )
= √ ( 3 * 0,5 ² )
= 0,5 * √ 3
= 0,866 m
Bezüglich des kürzesten Krabbelweges könnte man nun leicht der Versuchung unterfallen anzunehmen, dass dieser der Weg FBD sei, der also von der oberen Ecken F an der Kante hinunter zur unteren Ecke B und von dort aus diagonal zur gegenüberliegenden Ecke D führt. Dieser Weg ist in dem folgenden Bild in rot eingezeichnet.
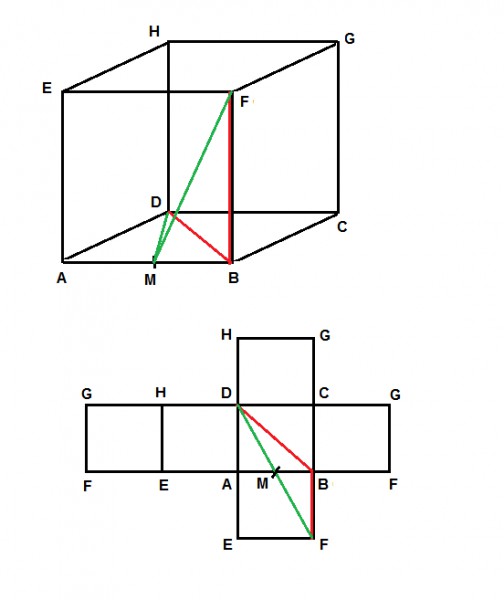
Wie man in der darunter gezeigten Würfelnetzabwicklung deutlich sieht, ist das jedoch nicht der kürzeste Weg. Statt dessen ist der kürzeste Weg derjenige, der in der Netzabwicklung eine gerade Linie bildet, also der Weg FMD. Dieser führt über den Mittelpunkt M der unteren Seite AB und ist in grün eingezeichnet.
Rechnet man nach, erhält man für den roten Weg Wrot
Wrot = FB + BD
= 0,5 + √ ( 0,5 2 + 0,5 2 )
= 0,5 + √ ( 2 * 0,5 2 )
= 0,5 + 0,5 * √ 2
= 0,5 * ( 1 + √ 2 ) = 1,207 m
und für den grünen Weg (dieser ist Hypotenuse des rechtwinkligen Dreiecks FED):
Wgrün = √ ( FE 2 + ED 2 )
=√ ( 0,5 2 + 1 2 )
= √ ( 1,25 ) = 1,118 m
(beide Werte gerundet).
Die Differenz beträgt knapp 0,09 m = 9 cm.