Berechne die Diagonale einer Raute

Question

Aufgabe

eine Raute eine Raute hat die Seitenlänge a = 2,5 cm und eine Diagonale e = 3 cm.

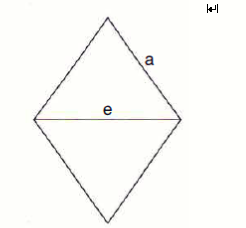
Mache eine Skizze, die auch die zweite Diagonale der Raute enthält und berechnen Sie die Länge der anderen Diagonalen.
b) Erkläre wie die gesamte Fläche und den Umfang der Raute berechnet wird.

Text erkannt:

\( \theta \)

Problem/Ansatz:

Kann mal jemand schauen, ob das so stimmt ?

Vielen Dank im Voraus

Zu a.)
a²= f²+e²  /-e²
f²= a³-e²
f²=6,25-2,25 / Wurzel ziehen
f= 2+2, f= 4cm

zu b.)
die Fläche mit der Formel A= 0,5*e*f berechnen
und den Umfang mit U= 4*a

Answer 1

Es gilt

(e/2)^2 + (f/2)^2 = a^2 --> f = √(4·a^2 - e^2) = √(4·2.5^2 - 3^2) = 4 cm

A = 1/2·e·f = 1/2·3·4 = 6 cm²

U = 4·a = 4·2.5 = 10 cm

Comments

Du gehst von a² = f² + e² aus. Das ist ja so verkehrt.

Answer 2

Hallo

a ist Hypotenuse im Dreieck e/2, f/2  damit ist a^2=e^2+f^2 falsch

allerdings hast du in a^2-e^2 nicht e^2 eingesetzt sondern (e/2)^2=2,25

dann hast du (f/2)^2=4,  f/2=2, f=4 also viele falsche Formeln und durch Zufall? am ende was richtiges.

b) du hast die richtige Formel, aber sie nicht erklärt!  du berechnest die Fläche der halben Raute als Fläche der 2 Dreiecke mit Höhe e/2 Grundseite f oder Höhe f/2 Grundseite f , oder zerlegst das untere Dreieck in 2 Hälften, die duoben links und rechts anlegst und hast ein Rechteck ,it Seite e und f/2

Gruß lul

Answer 3

a)

f= 2+2, f= 4cm

Ist richtig, nur der Rest ist glaube ich falsch.

(f/2)^2=6,25-2,25

2^2=4= 6,25-2,25

wäre richtig

(f/2)^2=a^2-(e/2)^2

(4/2)^2=(5/2)^2-(3/2)^2

wäre auch richtig

(2a)^2=f^2+e^2

5^2= 4^2+3^2

wäre auch richtig

b)

A= 0,5*e*f

A=0,5*4*3=6cm^2

U=4*a

U=4*2,5= 10cm