Fehlende Koordinate des Einheitsvektors bestimmen

Question

Aufgabe:

Bestimme die fehlende Koordinate des Einheitsvektors (Es gibt zwei Möglichkeiten).

a_{0= (0,28 Ι r)  r=?}

Problem/Ansatz:

Kann mir jemand helfen und de Rechenweg erklären, verstehe diese Aufgabe nicht. Vielen Dank!

Answer 1

Aloha :)

Ein Einheitsvektor hat immer die Länge \(1\). Daher muss gelten:

$$1\stackrel!=\left\|\binom{0,28}{r}\right\|=\sqrt{0,28^2+r^2}\quad\Rightarrow\quad1=0,28^2+r^2\quad\Rightarrow\quad r^2=1-0,28^2$$$$\Rightarrow\quad r=\pm\sqrt{1-0,28^2}=\boxed{\pm0,96}$$

Answer 2

Hallo,

Willkommen in der Mathelounge!

Schau Dir bitte folgende Skizze an:

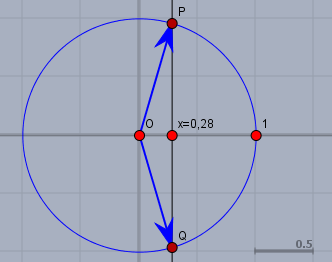
Gesucht ist ein Einheitvektor - also ein Vektor der Länge 1. Beginnend vom Punkt \(O\) muss die Spitze des Vektors also auf dem blauen Kreis liegen. Wir wissen, dass seine X-Koordinate den Wert \(0,28\) hat. Folglich muss seine Spitze dann auch auf der senkrechten schwarzen Geraden liegen.

Diese Gerade schneidet den blauen Kreis in den Punkten \(P\) und \(Q\). Wenn man die Y-Koordinate berechnen möchte, so gilt für das rechtwinklige Dreieck \(OXP\) der Satz von Pythagoras - also ist: $$\begin{aligned} 0,28^2 + y^2 &= 1 \\ y^2 &= 1 - 0,28^2 = 0,9216 \\ y &= \pm \sqrt{0,9216} = \pm 0,96\end{aligned}$$Demnach sind die beiden möglichen Einheitsvektoren$$a_0 = \begin{pmatrix} 0,28 \\ 0,96 \end{pmatrix}, \quad a_1 = \begin{pmatrix} 0,28 \\ -0,96 \end{pmatrix}$$