Aufgabe:
Ich fotografiere die Aufgabe einmal ab, weil ich sonst nicht wüsste, wie ich das hier so darstellen könnte:
Text erkannt:
Bestimmen Sie die fehlende Koordinate so, dass \( \vec{a} \perp \vec{b} \).
\( \vec{a}=\left(\begin{array}{l}2 \\ 3 \\ 0\end{array}\right), \vec{b}=\left(\begin{array}{r}b_{1} \\ -4 \\ 3\end{array}\right) \)
b) \( \vec{a}=\left(\begin{array}{c}1 \\ a_{2} \\ 3\end{array}\right), \vec{b}=\left(\begin{array}{r}2 \\ -1 \\ 1\end{array}\right) \)
c) \( \vec{a}=\left(\begin{array}{r}-1 \\ 4 \\ 2\end{array}\right), \vec{b}=\left(\begin{array}{c}3 \\ 0 \\ b_{3}\end{array}\right) \)
Problem/Ansatz:
Zu der Aufgabe habe ich schon einen Ansatz: ich habe das Skalarprodukt gebildet und es 0 gesetzt. Jetzt muss ich b1, a2, b3 so setzen, dass 0 rauskommt, aber das kriege ich nicht so richtig hin. Könnte mir da vielleicht jemand helfen? Sonst habe ich es auch verstanden:
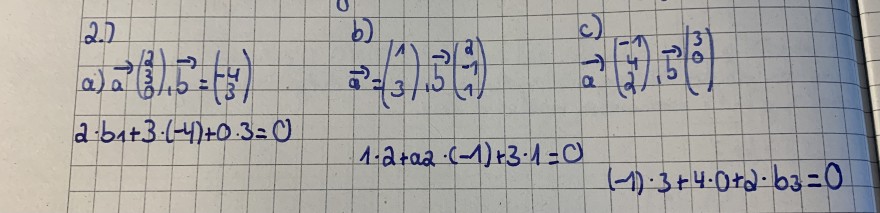
Text erkannt:
2.)
a) \( \vec{a}\left(\begin{array}{l}2 \\ 3 \\ 0\end{array}\right), \vec{b}=\left(\begin{array}{c}-4 \\ 3\end{array}\right) \)
b)
c)
\( 2 \cdot b_{1}+3 \cdot(-4)+0 \cdot 3=0 \)
\( \vec{a}=\left(\begin{array}{l}1 \\ 3\end{array}\right), \vec{b}\left(\begin{array}{c}2 \\ -1 \\ 1\end{array}\right) \)
\( \vec{a}\left(\begin{array}{c}-1 \\ 4 \\ 2\end{array}\right), \vec{b}\left(\begin{array}{l}3 \\ 0\end{array}\right) \)
\( 1 \cdot 2+a_{2} \cdot(-1)+3 \cdot 1=0 \)
\( (-1) \cdot 3+4 \cdot 0+2 \cdot b_{3}=0 \)