Hallo,
(jetzt habe ich doch ein wenig Zeit!)
Die Aufgabe ist deshalb so schön, weil man die Mathematik, die zur Lösung führt, erst finden muss. Beim Thema Graphentheorie stellt sich immer die Frage: was sind die Knoten und was die Kanten des Graphen?
Man könnte jeder Stellung einem Knoten und jeder Kante einen Springerzug zuweisen. Wenn ich mich nicht verrechnet habe, sind das 420 Knoten und von jedem Knoten gehen 2 bis 8 Verbindungen zu anderen Knoten. Dann wäre zu zeigen, dass dies kein zusammenhängender Graph ist und die beiden Stellungen in zwei unterschiedlichen Untergraphen hängen. Aber die Zahl 420 ist einfach zu groß - oder?
Das Hauptproblem ist doch hier:
Das Problem liegt bei den anderen Springer, denn die stehen immer im Weg.
Wenn Springer A an Springer B vorbei will, kommt er u.U. nicht vorbei. Das ist doch so wie auf einer Straße mit nur einer Fahrbahn. Man kann nicht überholen und ist gezwungen hinter dem Vordermann hinterher zu dackeln.
Tipp: finde diese Straße!
Falls Du es in 30min nicht geschafft hast, öffne den Spoiler
[spoiler]
Ich bezeichne die Felder so, wie es im Schach üblich ist.
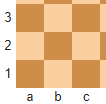
Da die Springer sich nur auf den 8 Randfeldern bewegen können, ordne ich die Felder in der folgenden Art und Weise im Kreis an und setze die beiden Springerpaare so darauf wie es in der ersten Stellung angegeben ist:
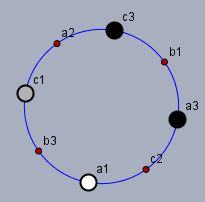
Die weißen Springer stehen auf den Feldern \(a1\) und \(c1\) und die schwarzen auf \(a3\) und \(c3\). Jeder Springer kann sich nur nach genau zwei Feldern bewegen. In dem obigen Kreis sind das die unmittelbar benachbarten. Kein Springer kann den anderen entfernen oder überholen.
Somit ist es auch nicht möglich, einen weißen Springer zwischen die beiden Schwarzen zu bringen, oder umgekehrt. Bei der zweiten Stellung sind aber die Springer auf \(c1\) und \(c3\) vertauscht. D.h. schwarze und weiße Springen stehen dann abwechselnd auf dem Kreis!
Daraus folgt, dass diese zweite Stellung durch Springerzüge und ohne die anderen zu schlagen nicht zu erreichen ist.
[/spoiler]