Hallo,
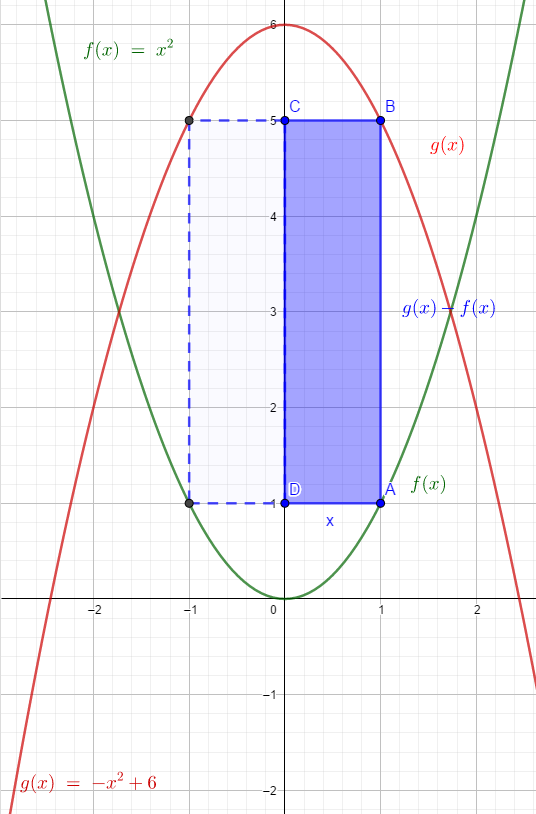
da die beiden Graphen symmetrisch zur y-Achse sind, genügt es, das blaue Rechteck ABCD zu betrachten.
Flächeninhalt \(A=x\cdot \big(g(x)-f(x)\big)\\=x\cdot(x^2-(-x^2+6))\)
Multipliziere die Klammer aus, bilde die 1. Ableitung, setze sie = null und löse nach x auf.
Du kannst dich gerne melden, falls du dazu noch Fragen hast.
Gruß, Silvia