Bestimmen Sie die Gleichung der Tangente t an den Graphen im Punkt P.

Question

Aufgabe:

Hallo ich komme da in Mathe gerade nicht weiter :(

Frage: P ist ein Punkt des Graphen f. Bestimmen Sie die Gleichung der Tangente t an den Graphen im Punkt P. An welcher Stelle schneidet die Tangente die x-Achse?

a) f mit f(x) = -x^2 ; P(2| f(2))

b f mit f(x) = 2x^2-x ; P(-3|f(-3)

Answer 1

f mit f(x) = -x^2 ; P(2| f(2))

Tangentensteigung m = f ' (2)    mit f ' (x) = -2x gibt das m = -4

und f(2) = - 2^2 = -4

Mit y = mx+n gibt es  -4 = -4*2 + n also n=4

==>  t: y = -4x+4

Sieht so aus ~plot~ -x^2; -4x+4;{2|-4}; [[-5|5|-8|2]] ~plot~

Der zweite sieht so aus ~plot~ 2*x^2-x; -13x-18;{-3|21}; [[-5|5|-20|30]] ~plot~

Answer 2

Hallo,

$$f(x)=2x^2-x\\f(-3)=21\\f'(x)=4x-^1$$

allgemeine Tangentengleichung: y = mx + b

m = Steigung = 1. Ableitung an dem Punkt

b = Schnittpunkt mit der y-Achse, den du bestimmst, indem du die Steigung und die Koordinaten des Punktes in die Gleichung einsetzt und nach b auflöst.

[spoiler]

$$f'(-3)=4\cdot (-3)-1=-13\\ y=-13x+b\\ 21=-13\cdot(-3)+b\\ 21=39+b\\-18=b\\\text{Gleichung der Tangente:}\\ y=-13x-18$$

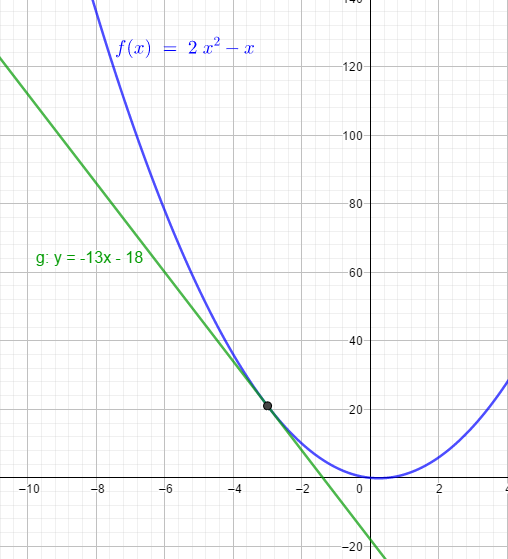
[/spoiler]

Gruß, Silvia