Für welche Werte von x (in cm) ist die Zielfunktion V(x) im Hinblick auf die Aufgabenstellung zu untersuchen?

Question

Aufgabe:

"Bestimmen der Definitionsmenge"

Für welche Werte von x (in cm) ist die Zielfunktion V(x) im Hinblick auf die Aufgabenstellung zu untersuchen?

Problem/Ansatz:

Wie berechne ich die Definitionsmenge? (noch nie gelernt wie das geht,bloß das maximale Volumen berechnen habe ich bis jetzt gelernt)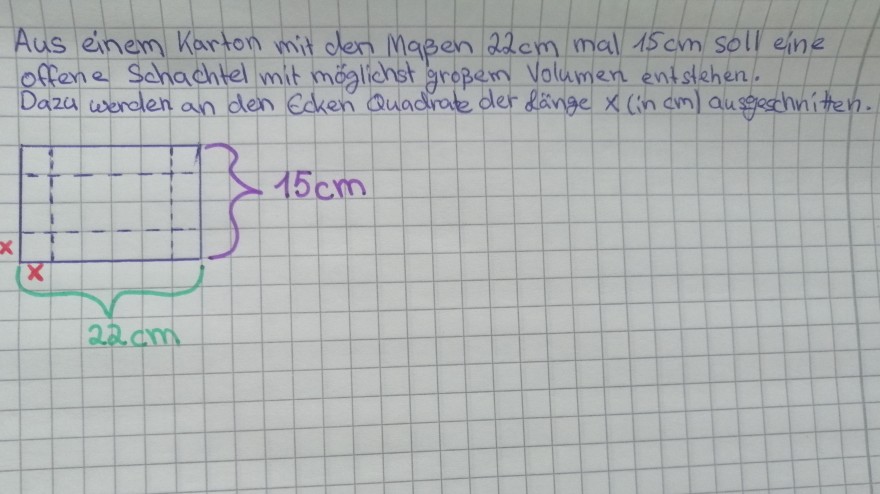

Text erkannt:

Aus einem Karton mit den Mapen \( 22 \mathrm{~cm} \) mal \( 15 \mathrm{~cm} \) soll eine offene schachtel mit móglichst gropem Volumen entstehen. Daza wenden an den Ecken Quadrate der dánge \( x \) (in \( \mathrm{cm} \) ) ausgechnitten.

Text erkannt:

Aus einem Karton mit den Mapen \( 22 \mathrm{~cm} \) mal \( 15 \mathrm{~cm} \) soll eine offene schachtel mit móglichst gropem Volumen entstehen. Daza wenden an den Ecken Quadrate der lainge \( x \) (in \( \mathrm{cm} \) ) ausgechnitten.

Answer 1

V(x) = (22 - 2·x)·(15 - 2·x)·x

D = [0 ; 7.5]

7.5 weil das die halbe Breite ist und mehr kannst du von der Breite nicht nach oben klappen.

Comments

Wie berechnet man das? Gibt es ein rechenweg dafür für eine solche Aufgabe?

---

Du könntest es dir Vorstellen.

Du kannst aber auch sagen das 15 - 2·x je die Breite der Grundfläche nach dem Hochklappen ist und dieser ausdruck nicht negativ werden darf

15 - 2·x ≥ 0 --> x ≤ 7.5

x selbst darf aber auch nicht negativ sein. Weil man kein Quatrat mit negativer Kantenlänge rausschneiden könnte.

x ≤ 7.5

Zeichne dir auch die Funktion. Macht es Sinn, wenn das Volumen sich im negativen Bereich befindet? Die Nullstellen der Funktion könnten also Aufschluss über den Definitionsbereich geben.

~plot~ (22-2x)(15-2x)x;[[-1|9|-50|500]] ~plot~