Jordan-Nullmenge des Sierpinski-Teppich

Question

Aufgabe:

Problem/Ansatz:

Hallo, soweit bin ich gekommmen, allerdings muss ich eigentlich zeigen, damit die Menge eine Jordan-Nullmenge ist, dass für alle epsilon das äußere Jordanvolumen echt kleiner epsilon ist. Ich weiß aber dann nicht, wie ich meine Zerlegung des Quaders vornehmen soll.

Answer 1

du bist grad bei Ana2 bei Prof. Ramacher, oder?

Ich sitze auch grad an der Aufgabe.

Ich denke, dass du da falsch ran gehst.

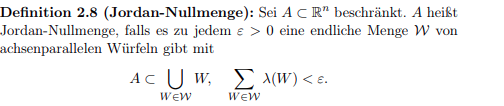
Text erkannt:

Definition 2.8 (Jordan-Nullmenge): Sei \( A \subset \mathbb{R}^{n} \) beschränkt. \( A \) heißt Jordan-Nullmenge, falls es zu jedem \( \varepsilon>0 \) eine endliche Menge \( \mathcal{W} \) von achsenparallelen Würfeln gibt mit
$$ A \subset \bigcup_{W \in \mathcal{W}} W, \sum \limits_{W \in \mathcal{W}} \lambda(W)<\varepsilon $$

Das hier ist die Definition einer Jordan-Nullmenge.

Ich weiß noch nicht ganz, wie, aber ich würde damit beginnen, zu zeigen, dass es eine Lebesgue-Nullmenge ist und damit die zweite Bedingung gilt.

Comments

Hallo Marburger Mathe-Kommilitone/Kommilitonin, :D

ja das war auch nur meine erste Überlegung, dass ich mit der Summe beschreiben kann, wie sich der Flächeninhalt für die Folge der Qn verhält. Nur bin ich dann nicht weiter gekommen wie ich eine entsprechende Zerlegung von Quadern wählen kann, sodass ich die eben von dir genannte Definition zeigen kann.

Die Idee mit Lebesque-Nullmenge klingt nicht so schlecht, nur dass ich schon am Freitag die Aufgabe bearbeiten habe und wir ja da noch nicht soweit gekommen sind und deswegen es noch nicht damit versucht habe:)

Problem dabei ist ja nur, dass ja nicht jede Lebesque-Nullmenge eine Jordan Nullmenge ist. Dann Ist die Frage, worin sich die Definitionen unterscheiden... Etwa nur um die Voraussetzung, dass A bei Jordan beschränkt sein muss und bei Lebesque nicht... Hmm die Aufgabe finde ich auch aktuell am schwierigsten.

Liebe Grüße

---

Also ich habe aktuell das so aufgeschrieben.

Ich meine, wenn ich irgendwie zuvor zeigen kann, dass der Teppich Jordan-Messbar ist, dann könnte ich sogar vielleicht wie hier im Bild einfach zeigen, dass das Jordan-Volumen 0 ist

. Das könnte natürlich wirklich der falsche Ansatz sein, vielmehr ist mir aber bis hin nicht eingefallen.... Ach und bei meinem Iduktionsanfang muss natürlich 8/9 stehen

---

Tatsächlich "nur" Physiker.

Und ich habe seit nem Jahr keinen Mathe Kurs mehr belegt, also bin ich mit allen Aufgaben (bis auf 1. und 2.) etwas am Hinken.

könnten wir im Notfall die 6. als bewiesen annehmen und es darüber machen? Ich glaub, die Mathe Profs mögen sowas nicht so gerne, oder?

Ansonsten: habe ihr Mathematiker ne Gruppe in die man rein kommen kann, wo man vielleicht Fragen stellen könnte?

---

Also die 6 habe ich mir gar nicht angeschaut, bin nämlich Lehramt Mathematik. Und nein, haben wir leider nicht, deswegen habe ich im Forum meines Tutoriums mal angefragt, ob wir eine Gruppe erstellen wollen und entsprechend meine Nummer reingeschickt.

Und ja das Übungsblatt ist aber auch echt scheiße, bin eh kein Fan von Analysis...

Und jaa halt wenn du eine vorherige Aufgabe bewiesen hast, dann kannst du die für die nächste nehmen. Aber anders herum weiß nicht, denke eher nicht.

---

Kurze Frage:

hab ich das jetzt richtig verstanden, dass wir da eigentlich grad das infimum des Volumens berechnet haben?

Denn, wenn wir das getan haben, und das =0 ist, müsste es nicht automatisch eine Jordan-Nullmenge sein?

Also ich mein mit deinem Beweis der Konvergenz des Volumens gegen 0.

Und ja. der Zettel ist heftig. Einige meiner Kommilitonen haben schon aufgegeben, weil sie, obwohl sie letztes Semester erst die Ana1 gemacht haben, noch weniger kapieren als ich (sprich: sie verstehen die Fragen nicht einmal)

---

Nee das Infinum habe ich mit der Reihe nicht berechnet, sondern wirklich das Jordan Volumen falls es existieren sollte.

Und jaa man muss froh sein, wenn man kein Mathe Genie ist, da erstmal das irgendwie zu bestehen.

---

Ach und falls du möchtest, kann du natürlich auch dann in die Mathe-Gruppe kommen. Schreib mir einfach eine Nachricht an meine Email: Brillm@students.uni-marburg.de

Answer 2

Definiere dir eine Folge von Mengen \(S_i = [0,1]^2 - Q_i\), dann gilt klarerweise: \(S = \bigcap S_i\), also auch: \(S\subseteq S_i\) für alle \(i\in\mathbb{N}\), anschaulich macht man sich das an den Bildern klar. Jetzt gilt aber \(\operatorname{vol}(S_0) = 1\) und \(\operatorname{vol}(S_{n+1}) = \frac{8}{9}\cdot \operatorname{vol}(S_n)\), das bedeutet also, dass \(\lim \operatorname{vol}(S_n) = 0\), es gibt also für jedes \(\varepsilon > 0\) ein \(n\) mit \(\operatorname{vol}(S_n)<\varepsilon\). Jetzt die obere Teilmengenbeziehung einsetzen und du weißt für alle \(\varepsilon > 0\):\(\operatorname{vol}(S) < \varepsilon\). Deine Würfelaufteilung folgt einfach daraus, dass du jedes \(S_n\) schreiben kannst als eine Vereinigung von \(8^{n}\) Würfeln mit Volumen \(\frac{1}{9}^n\).