Lineare Gleichungssystem: Werte von a

Question

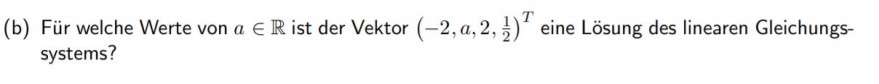
Text erkannt:

(b) Für welche Werte von \( a \in \mathbb{R} \) ist der Vektor \( \left(-2, a, 2, \frac{1}{2}\right)^{T} \) eine Lösung des linearen Gleichungssystems?

Hier habe ich eine erweiterte Matrix mit dem Vektor aus b) auf die rechte Seite erstellt.

Anschließend habe ich nach dem Gauß- Verfahren für die letzte Zeile (0 0 0 0 | 6 ) raus bekommen. Das bedeutet das es keine Lösung gibt, da Rg(A)= 3 < Rg(A|b) = 4.

Existiert jetzt demnach kein a ∈ R für das eine Lösung gibt ?

Answer 1

Ich bekomme Lösungen der Form

8-5t
-2+2t
t
1/2

also wäre bei b) a=2

Comments

Das erste Ergebnis habe ich auch nur das mit a=0 kann ich nicht nachvollziehen woran stellt man das fest ?

---

Vergleiche

8-5t     und  -2
- 2+2t   und a
t          und 2
1/2        und 1/2

also t=2 und damit -2+2t = 2

Oha, da hatte ich mich vertan  a=2 ist richtig.