Bestimme die gemeinsame Verteilung von X und Z := max{X,Y}.

Question

Aufgabe:

Gegeben seien zwei unabhängige zufällige Größen X,Y. Wir nehmen an, dass sie die gleiche
geometrische Verteilung besitzen (X ∼ Geo_q,Y ∼ Geo_q), d.h.
pX (k) = pY (k) = (1−q)q^k    für k = 0,1,2,....

(a) Bestimme die gemeinsame Verteilung von X und Z := max{X,Y}.

(b) Bestimme die Verteilung von Z.

Könnte mir jemand helfen bitte die Aufgaben zu lösen?


Vielen :)

Answer 1

Probiere doch zunächst einmal \(P_{X,Z}(0;0)\), \(P_{X,Z}(0;1)\), \(P_{X,Z}(0;2)\), \(P_{X,Z}(1;0)\), \(P_{X,Z}(1;1)\), \(P_{X,Z}(1;2)\) usw. zu berechnen, um dir einen Überblick zu verschaffen. Du solltest erkennen, dass die gemeinsame Verteilung folgende Form haben muss:

$$ P_{X,Z}(x,z)= \begin{cases} f_1(x,z) &\text{, für }x>z\\ f_2(x,z) &\text{, für }x=z\\ f_3(x,z) &\text{, für }x<z \end{cases} $$

Kannst du zunmindest \(f_1\) bestimmen, vielleicht auch \(f_3\)?

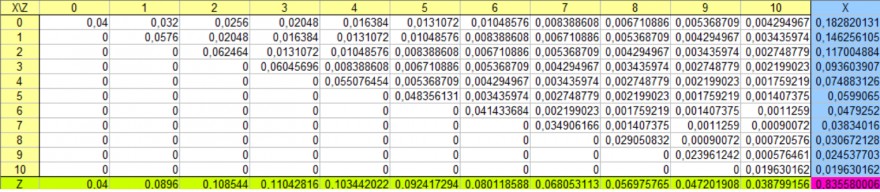
Hier ist ein Ausschnitt der Verteilung für \(q=0,8\), damit du deine Überlegungen überprüfen kannst:

Comments

Kannst du bitte mit der Lösung anfangen? dann kann ich vielleicht verstehen und selbst weiter machen :)

---

\(P_{X,Z}(0,0)\) bedeutet doch: die Whk., dass \(X=0\) ist und \(Z=0\) ist. \(Z\) wiederum ist das Maximum von \(X\) und \(Y\), also gilt \(\text{max}(0,Y)=0\), was wiederum bedeutet, dass auch \(Y=0\) gelten muss.

Somit ergibt sich

\(P_{X,Z}(0,0)=P_{X,Y}(0,0)=(1-q)q^0 \cdot (1-q)q^0=(1-q)^2\)

Für \(q=0,8\) ergibt sich demnach \(P_{X,Z}(0,0)=(1-0,8)^2=0,04\), wie du in der Tabelle obenlinks nachprüfen kannst.

---

Vielen Dank! :)