kurze Frage, warum kann man hier laut Lösung einfach mit der Funktion (+2 nach oben verschoben) rechnen?
Danke

Text erkannt:
16. Die Fläche, die der Graph von \( f \) mit \( f(x)=x^{3}-3 x \) mit der Tangente im Tiefpunkt einschließt, rotiert um die Tangente im Tiefpunkt. Dabei entsteht ein zwiebelförmiger Körper. Berechnen Sie sein Volumen.
Text erkannt:
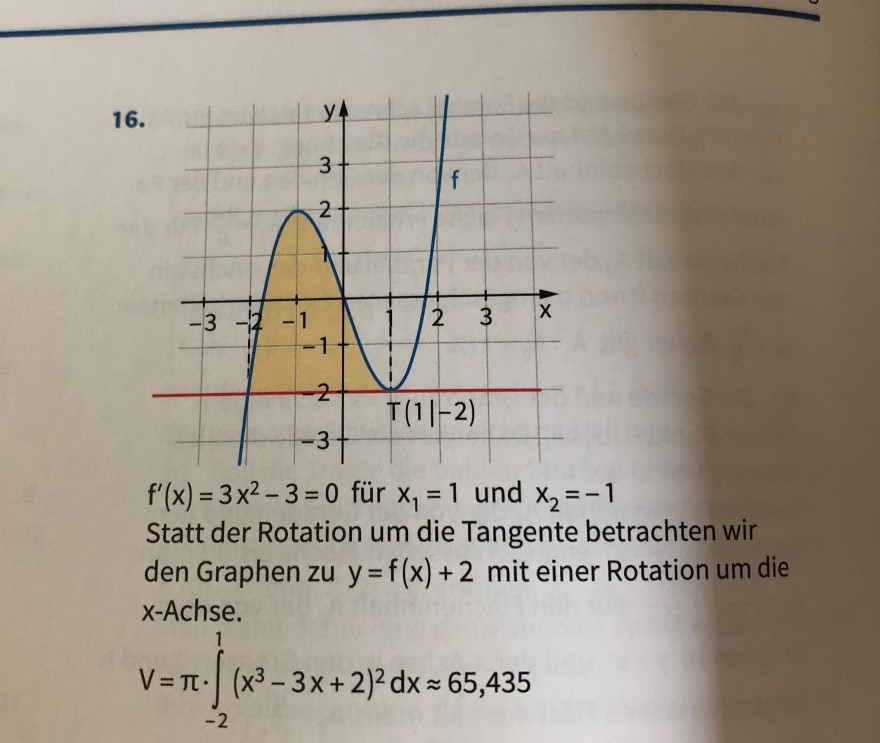
\( 16 . \)
\( f^{\prime}(x)=3 x^{2}-3=0 \) für \( x_{1}=1 \) und \( x_{2}=-1 \)
Statt der Rotation um die Tangente betrachten wir den Graphen zu \( y=f(x)+2 \) mit einer Rotation um die \( x \) -Achse. \( V=\pi \cdot \int \limits_{-2}^{1}\left(x^{3}-3 x+2\right)^{2} d x \approx 65,435 \)