Wie bestimme ich ganzrationale Zahlen mit vorgegebenen Eigenschaften?

Question

wie skizziere ich den Graphen einer Funktion f für x>0, der durch den koordinatenursprung verläuft und dessen Steigung zunächst größer und dann kleiner und anschließend sogar negativ wird?

Besten Gruss

Comments

Du suchst anscheinend die Funktionsgleichung einer ganzrationalen Funktion.

Oder doch nur eine Skizze?

Answer 1

Hi

------------------------------------------------------------------------------------------------------------------------------------------------

Was hat das mit ganzrationalen Zahlen zu tun?

Answer 2

 

der Graph von f(x) soll durch den Koordinatenursprung verlaufen (dann ist allerdings x nicht > 0, sondern = 0):

f(0) = 0

Die Steigung soll anfänglich größer werden, deshalb können wir z.B. sagen

f'(0) = 1

f'(1) = 2

Dann soll die Steigung kleiner und schließlich sogar negativ werden:

f'(2) = -1

 

Wir haben 4 Informationen, können also eine Funktion 3. Grades aufstellen:

f(x) = ax³ + bx² + cx + d

f'(x) = 3ax² + 2bx + c

 

Wir setzen ein:

f(0) = 0 = d

f'(0) = 1 = c

f'(1) = 2 = 3a + 2b

f'(2) = -1 = 12a + 4b + c

 

a = -1

b = 2,5

c = 1

d = 0

 

Die Funktionsgleichung lautet also

-x³ + 2,5x² + x

 

 

Diese Funktion (unter unendlich vielen) sollte die von Dir angegebenen Bedingungen erfüllen.

 

Besten Gruß

Comments

Hi Brucybabe!

Damit Du Dich nicht schlaflos grübelnd durch die Nacht quälen musst, von wem der Pluspunkt wohl sein mag, das war ich! ;) :P

---

Hi gorgar,

danke für den Pluspunkt und danke für die Info - die Nacht ist gerettet!!

Einfache Lösungen sind aber immer noch die besten, deshalb möchte ich auch Dir ein - letztendlich sinnloses - Grübeln ersparen: + von mir :-D

---

Bis dahin konnte ich folgen.

Ich versteh nicht a = -1 , b= 2,5 , c= 1 und d = 0.
Woher kommen diese Zahlen?

---

@Anonym:

Eine Funktion 3. Grades lautet allgemein:

f(x) = ax³ + bx² + cx + d

mit der 1. Ableitung

f'(x) = 3ax² + 2bx + c

Nun habe ich die Bedingungen eingesetzt:

f(0) = 0, also a*0³ + b*0² + c*0 + d = 0 | also d = 0

f'(0) = 1, also 3a*0² + 2b*0 + c = 1 | also c = 1

f'(1) = 2, also 3a*1² + 2b*1 + c = 2

f'(2) = -1, also 3a*4 + 2b*2 + c = -1

 

Jetzt habe ich vier Gleichungen mit 4 Unbekannten:

d = 0

c = 1

3a + 2b + c = 2

12a + 4b + c = -1

 

Nun muss ich mich korrigieren:

a = -2/3

b = 1,5

c = 1

d = 0

 

Damit lautet die Funktion

-2/3 * x³ + 1,5 * x² + x

 

und sieht so aus:

 

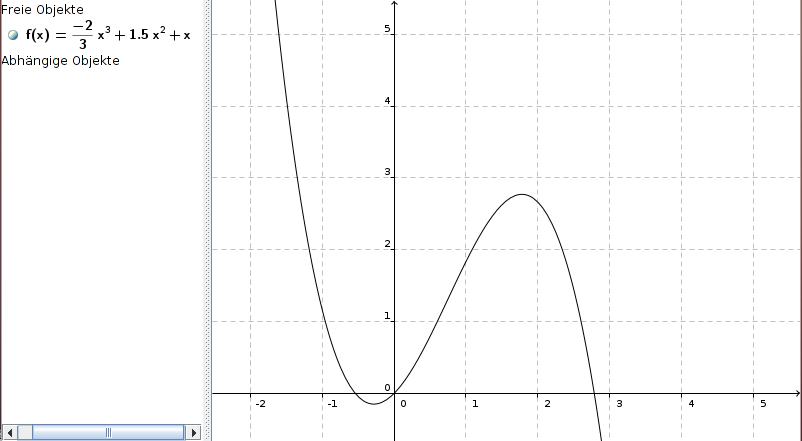
Sorry für die falsche Berechnung - ich hoffe, jetzt ist die Vorgehensweise klar geworden :-)

---

Ja bite. Noch eine letzte frage quält mein Anliegen. Nämlich wie errechnet man a = -2/3 und b = 1,5?

---

Nicht quälen bitte :-)

 

Folgendes hatten wir:

I. d = 0

II. c = 1

III. 3a + 2b + c = 2

IV. 12a + 4b + c = -1

 

Damit reduzieren sich III. und IV. zu

V. 3a + 2b + 1 = 2, also 3a + 2b = 1

VI. 12a + 4b + 1 = -1, also 12a + 4b = -2

 

V. * 4 = 12a + 8b = 4

Das subtrahieren wir von VI. und erhalten

-4b = -6

4b = 6

b = 6/4 = 3/2 = 1,5

 

Das setzen wir zum Beispiel in V. ein:

3a + 2b = 1

3a + 3 = 1

3a = -2 | :3

a = -2/3

 

Nachvollziehbar?

Wenn nicht, bitte nochmals nachfragen :-)

---

Hallo.
Nicht ganz.
Nach der Reduktion, hast du geschrieben: V. * 4=12a + 8b = 4.
Würdest du mir bitte diesen Rechenschritt verdeutlichen?

Vielen Dank ?

---

Die Gleichung Nr. V lautete

3a + 2b = 1

Wenn ich die linke Seite mit einer Konstanten multipliziere und die rechte Seite mit der gleichen Konstante, ändert sich an der Gleichheit nichts! Ich habe also, um links auf 12a zu kommen und dies dann mit Gleichung Nr. VI verarbeiten zu können, beide Seiten mit 4 multipliziert:

4 * (3a + 2b) = 4 * 1 | ausmultiplizieren

12a + 8b = 4

 

Und diese "neue Gleichung" habe ich dann von Gleichung Nr. VI subtrahiert:

12a + 4b = -2

- (12a + 8b = 4)

mit dem Ergebnis

-4b = -6

Auch dies ist erlaubt und sinnvoll :-)