Hallo Cron,
wahrscheinlich hat Dir noch niemand geantwortet, weil die Aufgabenstellung unklar ist. Wahrscheinlich geht es darum, einen Fluß der Breite \(b_f=100\, \text m\) mit einem Boot zu überqueren, welches mit einer Geschwindigkeit von \(v_B=4\,\text {m/s}\) unterwegs ist. Die Fließgeschwindigkeit ist \(v_F=3\, \text{m/s}\). Weiter ist es wohl so, dass das Boot den kürzesten Weg, aber nicht die kürzeste Zeit wählen soll.
Dazu eine Skizze:
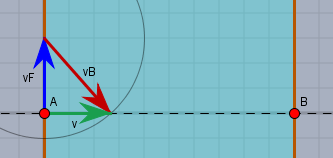
An der Geschwindigkeit \(v_F\) (blauer Vektor) des Flusses kann man nichts ändern. Wenn das Boot auf der Linie zwischen \(A\) und \(B\) bleiben soll, muss es mit seiner Geschwindigkeit \(v_B\) (rot) dagegen anfahren. Und zwar genau so weit, dass es auf der markierten Linie bleibt.
In der zeichnerischen Konstruktion erreicht man dies, indem man um die Spitze von \(v_F\) einen Kreis mit dem Radius \(|v_B|\) schlägt. Der Schnittpunkt mit der Gerade \(AB\) ist dann die Spitze des resultierenden Vektors \(v\) (grün). Es gilt in jedem Fall$$v = v_F + v_B, \quad v_F = \begin{pmatrix}0\\ 3\end{pmatrix}$$\(v\) soll in Richtung der X-Achse laufen. Das bedeutet, dass die Y-Koordinate \(v_y\) von \(v\) gleich 0 ist. Also $$v = \begin{pmatrix}v_x\\ 0\end{pmatrix}$$Die X-Koordinate \(v_x\) ist noch unbekannt. Nun löst man die erste Gleichung nach \(v_B\) auf und setzt das \(v\) ein:$$\begin{aligned} v &= v_F + v_B \\ v_B &= v - v_F \\ \begin{pmatrix}v_{Bx}\\ v_{By}\end{pmatrix} &= \begin{pmatrix}v_x\\ 0\end{pmatrix} - \begin{pmatrix}0\\ 3\end{pmatrix} = \begin{pmatrix}v_x\\ -3\end{pmatrix} \\ \implies v_{By} &= -3\end{aligned}$$Das \(v_{By}\) folgt aus der letzten Zeile der Vektorgleichung.
Und anschließend wird nur noch ausgenutzt, dass der Betrag der Bootsgeschwindigkeit \(|v_B|\) bekannt ist. Da ist noch ein kleiner Fehler in der Rechnung. Es muss heißen:$$|v_{Bx}| = \sqrt{ v_B^2 - v_{By}^2} = \sqrt{4^2- (-3)^2} = \sqrt 7$$\(v_{Bx}\) ist auch kein Vektor, sondern nur die X-Koordinate des Vektors.
Falls noch etwas unklar ist, so melde Dich bitte.