Kurvendiskussion für ganzrationale Funktion: f(x) = x^3 + 8x^2 - 7/2 x

Question

Aufgabe: Kurvenuntersuchung

Gegeben ist die ganzrationale Funktionen \( f(x)=x^{3}+8 x^{2}-\frac{7}{2} x ; x \in \mathbb{R} \)

a) Untersuchen Sie den Graphen der Funktion auf Symmetrie. Begründen Sie Ihre Aussage.

b) Untersuchen Sie das Verhalten der Funktionswerte von \( f \) im Unendlichen.

c) Bestimmen Sie die Koordinaten des Schnittpunktes mit der y-Achse.

d) Berechnen Sie die Nullstellen.

e) Berechnen Sie die Extrempunkte.

f) Berechnen Sie die Wendepunkte.

Problem/Ansatz:

Ich habe die Kurvenuntersuchung nur teilweise verstanden und würde gerne sehen wie man das löst.

Answer 1

a)

Keine Symmetrie bedingt durch gerade und ungerade Exponenten von x.
f(- x) = - x^3 + 8·x^2 + 3.5·x ≠ ± f(x)

b)
lim (x → - ∞) x^3 + 8·x^2 - 3.5·x = - ∞
lim (x → ∞) x^3 + 8·x^2 - 3.5·x = ∞

c)
Y-Achsenabschnitt: f(0)
f(0) = 0 → (0 | 0)

d)
Nullstellen: f(x) = 0
f(x) = x^3 + 8·x^2 - 3.5·x = x·(x^2 + 8·x - 3.5) = 0
x = 0
x = -4 ± √(16 + 3.5) → x = -12.42 ∨ x = 0.4159 → Das würde bereits als Begründung zu a) langen.

e)
Extrempunkte: f'(x) = 0
f'(x) = 3·x^2 + 16·x - 3.5 = 0
x = (-16 ± √(16^2 - 4·3·(-3.5)))/(2·3) = x = - 8/3 ± √298/6 → x = - 5.544 (VZW + nach -) ∨ x = 0.2104 (VZW - nach +)
f(- 8/3 - √298/6) = 149/54·√298 + 1276/27 = 94.89 → HP(- 5.544 | 94.89)
f(- 8/3 + √298/6) = 1276/27 - 149/54·√298 = - 0.3729 → TP(0.2104 | - 0.3729)

f) Wendepunkte: f''(x) = 0
f''(x) = 6·x + 16 = 0 → x = - 8/3 = - 2.667 (VZW - nach +)
f(- 8/3) = 1276/27 = 47.26 → WP(- 2.667 | 47.26)

Answer 2

Hallo,

Symmetrie:

Der Graph einer reellen Funktion ist

achsensymmetrisch zur y-Achse, wenn gilt f(-x) = f(x)

punksymmetrisch zum Ursprung, wenn gilt f(-x) = - f(x)

b) Das Grenzverhalten ist bei einer Funktion der Form f(x) = axⁿ durch den Koeffizienten a_n und den Grad der Funktion. Bei Bedarf bitte nachfragen.

c) Schnittpunkte mit der y-Achse ermittelst du, wenn du für x null einsetzt.

d) Setze die Gleichung = null und löse nach x auf

e) Extrempunkte: notwendige Bedingung ist f'(x) = 0

Die Ergebnisse für x in die zweite Ableitung einsetzen. Wenn f''(x) < =, handelt es sich um einen Hochpunkt. Wenn f''(x) > 0, handelt es sich um einen Tiefpunkt. Um die y-Koordinaten des Punktes/der Punkte zu bestimmen, den x-Wert in die Ausgangsleichung einsetzen.

f) Wendepunkte: notwendige Bedingung ist f''(x) = 0, anschließend prüfen, ob f'''(x) ≠ 0, y-Koordinate wie oben bestimmen.

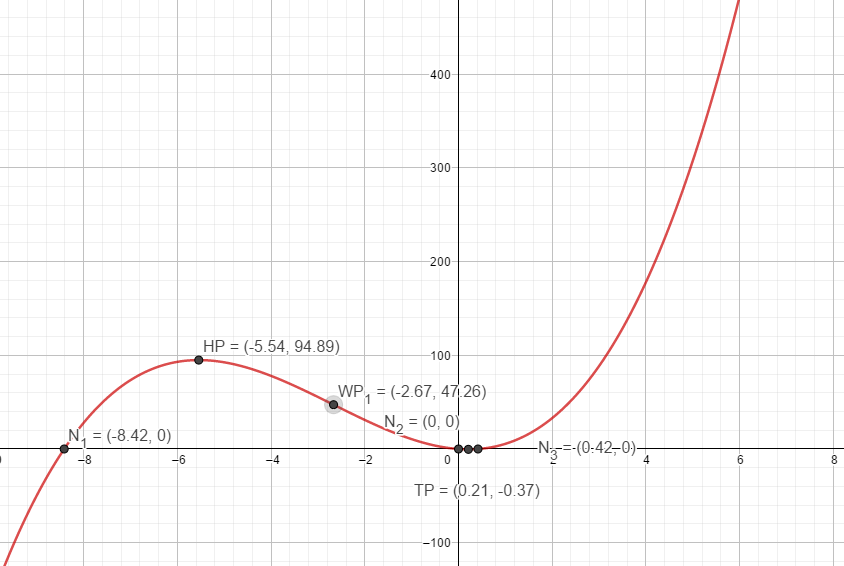
Gruß, Silvia