Bestimmen Sie den Beobachtungszeitraum, in dem die Sonnenblume am schnellsten bzw am langsamsten wuchs.

Question

Aufgabe:

Maria untersucht das Höhenwachstum ihrer Sonnenblume innerhalb von 200 Tagen. Sie hält die Wachstumsentwicklung in einer Tabelle fest:

Zeit t in Tagen	0	10	25	50	100	125	150	200
Höhe h in cm	0	12	39	73	124	140	160	192

a) Bestimmen Sie den Beobachtungszeitraum, in dem die Sonnenblume am schnellsten bzw. am langsamsten wuchs.

Problem/Ansatz:

Ich habe gemäß der Wertetabelle die Funktion eingezeichnet. Danach habe ich mir die Abstände zwischen den einzelnen Werten angeschaut und habe festgestellt das wohl möglich bei 50 Tagen und 73 cm (am schnellsten) ein Wendepunkt ist, sowie bei 125 Tagen und 140 Tagen (wird wieder langsamer).

Allerdings weiß ich jetzt nicht wirklich, wie ich da weiter machen soll. Muss ich da eine graphische Ableitung machen, wenn ja wie? Kann ich das auch rechnerisch machen?

Denn mein Problem ist, dass ich derzeit in Quarantäne bin und mich komplett selbstständig in die Differentialrechnung einarbeiten muss.

Ich habe mal im Anhang ein Foto von meiner Funktion.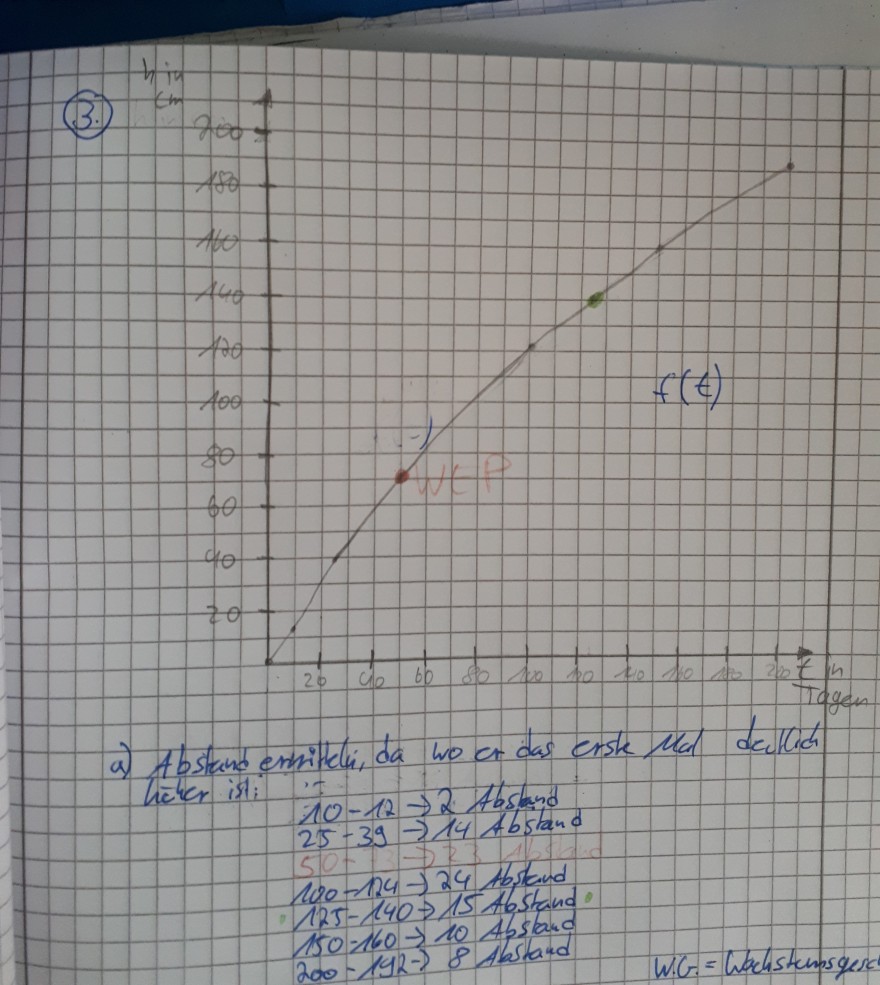

Text erkannt:

herer ist

Comments

Das hat (noch) nicht wirklich mit Differenzialrechnung zu tun. Die Blume wuchs dann am schnellsten, wo die Steigung am steilsten ist. Die Steigung in jedem Zeitraum kann man ausrechnen.

---

Und wie rechne ich die Steigung bei einem Zeitraum aus?

---

Unterschied in Richtung der y-Achse dividiert durch Unterschied in Richtung der x-Achse.

---

Ach so, dass ist die Sache mit Dy / Dx

Answer 1

Bestimme rechnerisch das Höhenwachstum in den 7 Intervallen über den Differenzenquotient.

m[0 ; 10] = (12 - 0)/(10 - 0) = 1.2 cm/Tag

Im Intervall der ersten 10 Tage wächst die Sonnenblume durchschnittlich um 1.2 cm/Tag. Wie sieht das in den anderen Intervallen aus? In welchem Intervall ist das durchschnittliche Höhenwachstum am schnellsten?

Comments

Ahh, das macht man also mit den Differenzenquotient, also
Dy / Dx. Vielen Dank!!

---

m[0; 10] = 1,2 cm / Tag
m[10; 25] = 1,8 cm / Tag
m[25;50] = 1,36 cm / Tag
m[50;100] = 1,02 cm / Tag
m[100;125] = 0,64 cm / Tag
m[125; 150] = 0,8 cm / Tag
m[150;200] = 0,64 cm/Tag

Am schnellsten: Zwischen den 10. und 25. Tag ist die durchschnittliche Wachstumsgeschwindigkeit (W.G.) mit 1,8 cm / Tag am schnellsten.

Am langsamsten: Zwischen den 100. und 125. Tag, sowie auch zwischen den 150. und 200. Tag lag die W.G: bei 0,64 cm / Tag.

---

Genau. Gut gemacht.