Aufgabe:
1/nWurzel(n!) zeigen sie den Grenzwert und die Konvergenz.
Problem/Ansatz:
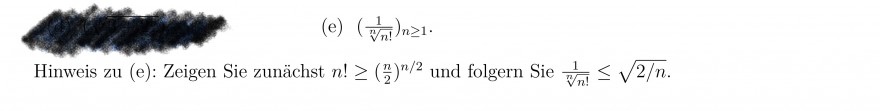
Text erkannt:
(e) \( \left(\frac{1}{\sqrt[n]{n} !}\right)_{n \geq 1} \)
Hinweis zu (e): Zeigen Sie zunächst \( n ! \geq\left(\frac{n}{2}\right)^{n / 2} \) und folgern Sie \( \frac{1}{\sqrt[n]{n !}} \leq \sqrt{2 / n} \).
Ich weiß leider gar nicht, wie ich beginnen soll. Das einzige, was ich weiss, ist dass √(n!) = ∞ daher sollte es gegen 0 konvergieren, dass n!>=√(n/2)^n ist ist klar, aber wie beweise ich es?