Skisprungschanze: Eine Anlaufbahn zum Schanzentisch bestimmen!.?

Question

Aufgabe:

Skisprungschanze

Der Verlauf des Schanzentisches lässt sich mit der folgenden Funktion beschreiben :

f(x) = 1/10x^2

0<x<6

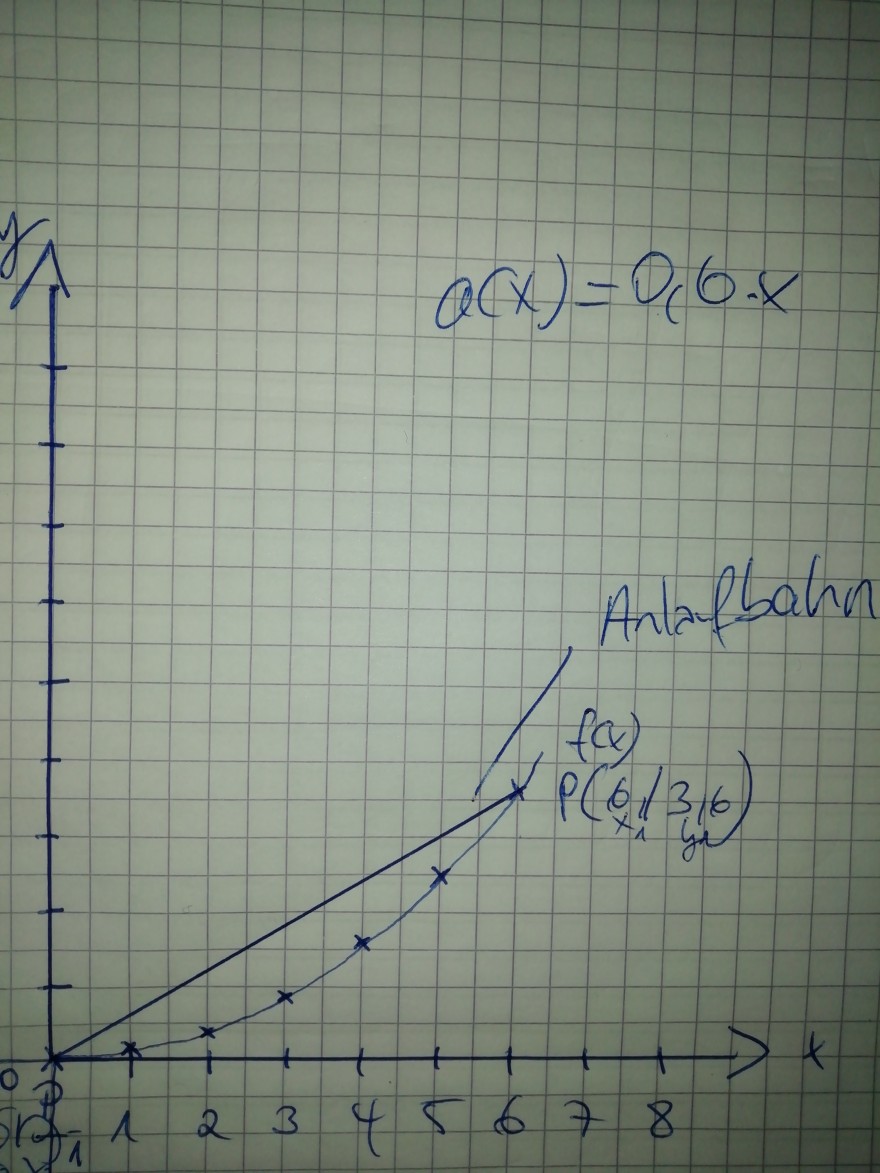
Man möchte eine Anlaufbahn bauen, die eine lineare Steigung hat und passend mit dem Schanzentisch abschließt.

1. Zeichen f(x) ins Koordinatensystem. Der Absprungspunkt liegt bei (0/0).

2. Zeichne an den höchsten Punkt P(6/3,6) eine Anlaufbahn, die sich eignen würde und Bestimme ihre Funktionsgleichung.

Problem/Ansatz:

Siehe Zeichnung/Anhang

Answer 1

Ich glaube, du sollst das eher so zeichnen. Macht doch mehr Sinn oder nicht?

Comments

Oh man, ja klar :)... Vielen Dank und dann wähle ich noch einen Punkt auf der Anlaufbahn und bestimme die Funktionsgleichung richtig? P(6/3,6) habe ich ja schon. Viele Dank!

---

Beachte das im Übergangspunkt (6 | 3.6) Schanzentisch und Anlaufbahn sowohl den gleichen Funktionswert als auch die gleiche Steigung haben müssen. Damit ist die Anlaufbahn eine Tangentiale Weiterführung der Funktion f im Punkt (6 | 3.6).