Aufgabe:
Gegeben ist der Vektorraum der reellen \( 2 x 2 \) -Diagonalmatrizen
\( V:=\left\{\left[\begin{array}{ll} a & 0 \\ 0 & b \end{array}\right] \mid a, b \in R\right\} \)
eine lineare Abbildung \( L: V \rightarrow V \) und die darstellende Matrix \( L_{\mathbb{B}} \) bezüglich einer Basis \( \mathbb{B}=\left\{B_{1}, \ldots, B_{n}\right\} \).
\( L \) und \( L_{\mathbb{B}} \) sind gegeben:
\( \left[\begin{array}{ll} v & \rightarrow \\ {\left[\begin{array}{ll} a & 0 \\ 0 & b \end{array}\right]} & \mapsto\left[\begin{array}{cc} a+5 b & 0 \\ 0 & -4 b \end{array}\right] \end{array}\right. \)
Die darstellende Matrix von \( L \) bezūglich einer Basis \( \mathcal{B} \) sei: \( L_{\mathscr{B}}=\left[\begin{array}{cc}-4 & -5 \\ 0 & 1\end{array}\right] \)
Geben Sie die Anzahl \( n \) der Elemente in der Basis \( B \) an und bestimmen Sie anschließend
Basiselemente für alle \( B_{i}(i=1, \ldots, n) \).
Bestimmen Sie eine Basis \( \mathcal{B} \), sodass \( L_{\mathscr{S}} \) die darstellende Matrix von \( L \) bzgl. \( \mathcal{B} \) ist.
(Hinweis: \( \mathscr{\text { ist nicht unbedingt eindeutig. D.h., es gibt unter Umständen mehr als eine }} \) mögliche Lösung.)
Ich hätte nun gesagt die Anzahl der Elemente in der Basis seien 2, danach weiß ich aber absolut nicht weiter (wie ich das berechnen soll). Aus meinen Aufzeichnungen werde ich auch nicht so ganz schlau... Hat jemand einen Ansatz?
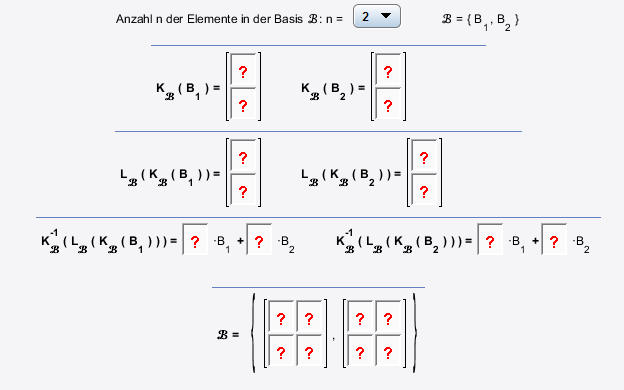
Lösungsfenster für n=2: