Hallo Leonie,
kannst Du eine Geradengleichung für den Lichstrahl \(l(t)\) aufstellen. Du brauchst nichts rechnen, vielmehr nur abschreiben, was in der Aufgabe steht:$$l(t) = \begin{pmatrix}-3\\ -1\\ 3\end{pmatrix} + \begin{pmatrix}1\\ 0\\ -1\end{pmatrix}t $$wenn der Lichtstrahl den Punkt \(A\) treffen soll, so muss ein \(t\) existieren, für das \(l(t)=A\) gilt. Schreiben wir's doch mal hin:$$l(t) = \begin{pmatrix}-3\\ -1\\ 3\end{pmatrix} + \begin{pmatrix}1\\ 0\\ -1\end{pmatrix}t = \begin{pmatrix}0\\ -1\\ 0\end{pmatrix}$$In der ersten Zeile der Vektorgleichung steht \(-3+t=0\). Kannst Du \(t\) 'handschriftlich' ausrechnen?
[spoiler]
Ist doch \(t=3\). Und wenn Du das in \(l(3)\) einsetzt, kommst Du zum Punkt \(A\). Und damit ist der Teil (a) schon erledigt!
[/spoiler]
Das sieht so aus:
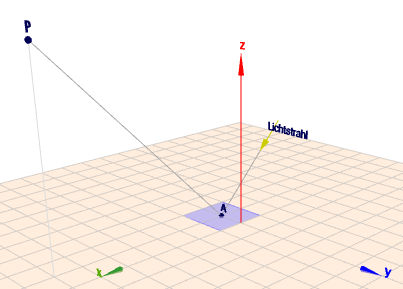
Wenn der Strahl nun von XY-Ebene reflektiert wird. Was bedeutet das für den Richtungsvektor der Geraden?
[spoiler]
Die Z-Richtung wird invertiert. Also verändert sich der Richtungsvektor, indem die Z-Koordinate invertiert wird:$$\begin{pmatrix}1\\ 0\\ -1\end{pmatrix} \to \begin{pmatrix}1\\ 0\\ 1\end{pmatrix}$$ Und die neue Geradengleichung startet in \(A\) mit der neuen Richtung:$$l'(t) = \begin{pmatrix}0\\ -1\\ 0\end{pmatrix} + \begin{pmatrix}1\\ 0\\ 1\end{pmatrix} t$$ nun prüfe nach, ob \(P\) auf der Geraden \(l'(t)\) liegt.
[/spoiler]
Nun ist noch nach der Ebene gesucht, in der sich der Lichtstrahl und seine Reflektion aufhält. Tipp: welche Koordinate hat sich auf dem ganzen Weg nicht verändert?
Falls Du irgendwo nicht weiter kommst, so melde Dich bitte.