Bestimme jenen Zeitpunkt, wo laut dem quadratischen Modell mehr Bakterien vorhanden sind als laut dem linearen Modell.

Question

Die Anzahl von Bakterien im Laufe der Zeit kann mit verschiedenen Modellen beschrieben werden, wie in der Abbildung zu sehen ist. (t gibt dabei die Zeit in Stunden an.)

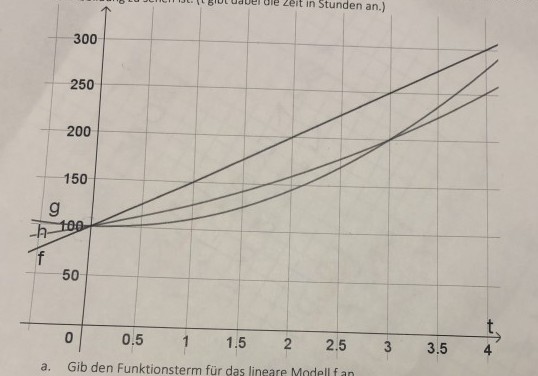
a) Gib den Funktionsterm für das lineare Modell \( f \) an.

b) Gib den Funktionsterm für das quadratische Modell \( \mathrm{g} \) an.

c) Gib den Funktionsterm für das exponentielle Modell h an.

d) Fülle die beiden Tabellen aus.

x	g(x)
	100
3

x	f(x)
	300
1

e. Bestimme jenen Zeitpunkt, wo laut dem quadratischen Modell mehr Bakterien vorhanden sind als laut dem linearen Modell.

f. Bestimme den Zeitpunkt wann laut dem exponentiellen Modell mehr als 1000 Bakterien vorhanden sind.

Meine Frage ist wie kann ich den Funktionsterm für das lineare Modelle quadratische Modell und exponentielle Modell angeben?

Answer 1

f(t) = 50·t + 100

g(t) = 100/9·t^2 + 100

h(t) = 100·2^{t/3}

Comments

Vielen lieben Dank!!

Können sie mir bitte noch erklären wie man auf die Funktionsterme kommt ?

Wie lesen Sie das ab bzw. wie kommt man auf die:

f(x) = 50·x + 100

g(x) = 100/9·x2 + 100

h(x) = 100·2^(x/3)

?

Answer 2

Ersichtlich ist die lineare Funktion mit
( 0 | 100 )
( 4 | 300 )
f = m * x + b

Quadratische Funktion
g = a * x^2 + 100
( 0 | 100 )
( 4 | 275 )

Expo
h = a * q^(t)
( 0  | 100 )
( 4 | 250 )

Jeweils 2 Gleichungen mit 2 Unbekannten
die es zu lösen gilt

links bei ( 0 | 100 ) sind die Bezeichner f,g,h für die
Graphen angegeben.

Es ist jetzt aber zu spät für mich.

Bei Bedarf nachfragen