Untersuchen Sie die Zahlenfolgen an auf Konvergenz

Question

Aufgabe:

Untersuchen Sie folgende Zahlenfolgen auf Konvergenz und bestimmen Sie ggf. den Grenzwert.

Problem/Ansatz:

a_n=1/n {\binom {n}{2}} Dort habe ich schon einen Ansatz, aber komme leider nicht weiter..

Vielen Dank für die Hilfe.

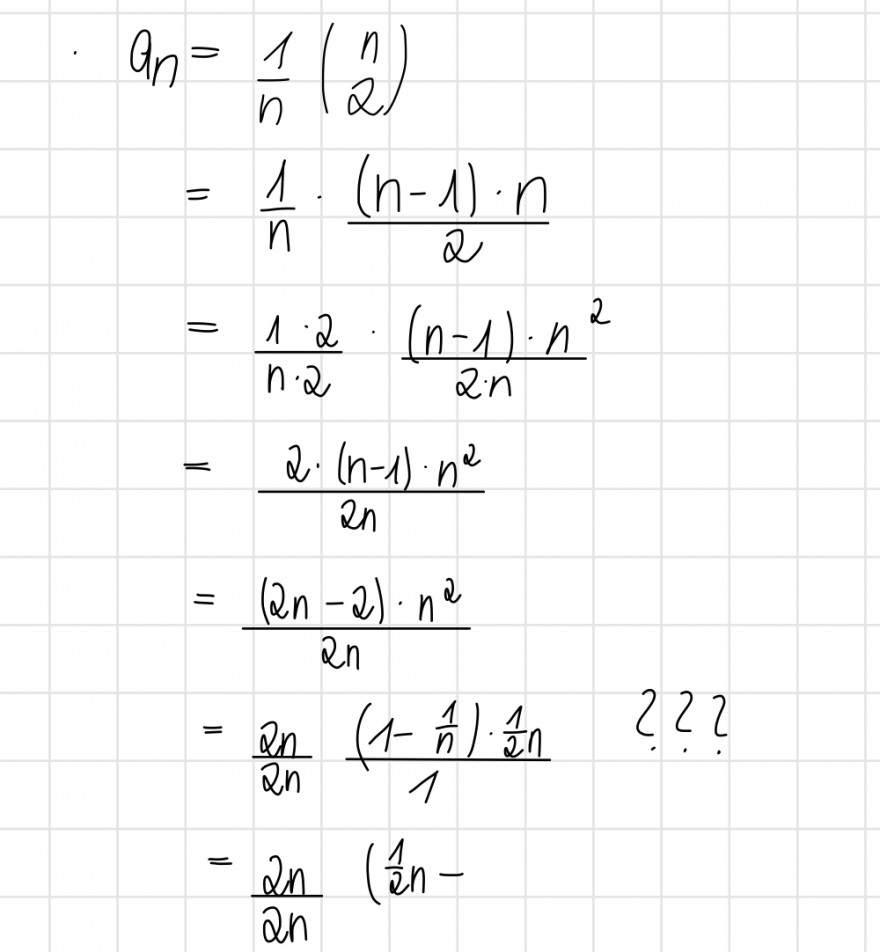
Text erkannt:

\( \begin{aligned} a_{n} &=\frac{1}{n}\left(\begin{array}{c}n \\ 2\end{array}\right) \\ &=\frac{1}{n} \cdot \frac{(n-1) \cdot n}{2} \\ &=\frac{1 \cdot 2}{n \cdot 2} \cdot \frac{(n-1) \cdot n^{2}}{2 \cdot n} \\ &=\frac{2 \cdot(n-1) \cdot n^{2}}{2 n} \\ &=\frac{(2 n-2) \cdot n^{2}}{2 n} \\ &=\frac{2 n}{2 n} \frac{\left(1-\frac{1}{n}\right) \cdot \frac{1}{2 n}}{1} \\ &=\frac{2 n}{2 n}\left(\frac{1}{2 n}-\right.\end{aligned} \)

Answer 1

Erinnere dich an die Definition des Binomialkoeffizienten: \(\begin{pmatrix} n \\ k \end{pmatrix}:=\frac{n!}{(n-k)!\cdot k!}\). dann gilt: $$\frac{1}{n}\begin{pmatrix} n\\2 \end{pmatrix}=\frac{1}{\cancel{n}}\cdot \frac{\cancel{n}(n-1)}{2}=\frac{n-1}{2}\xrightarrow{n\to \infty}\infty$$

Comments

Könnten Sie mir sagen, wo ich einen Fehler in meiner Rechnung gemacht habe?

---

Bereits im zweiten Schritt. Du kannst das \(n\) einfach kürzen, vgl. oben.

---

Achso okay, ja vielen lieben Dank. Ich habe so viele Aufgaben gerechnet und immer nach dem selben Prinzip, dass ich es hier auch so versuchen wollte und das vollkommen übersehen haben. Dankeschön!