Aufgabe:
Satz von Peano und Eindeutigkeit.
Wir betrachten das Anfangswertproblem y´ = f(x, y), y(0) = 0 mit der rechten Seite
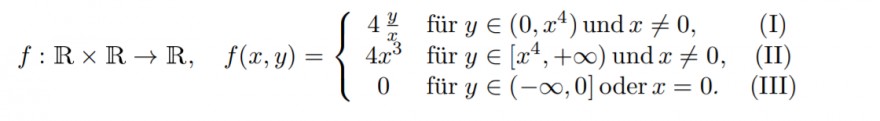
Text erkannt:
\( f: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{cl}4 \frac{y}{x} & \text { für } y \in\left(0, x^{4}\right) \text { und } x \neq 0, \\ 4 x^{3} & \text { für } y \in\left[x^{4},+\infty\right) \text { und } x \neq 0, \quad \text { (I) } \\ 0 & \text { für } y \in(-\infty, 0] \text { oder } x=0 .\end{array}\right. \)
a) Zeigen Sie, dass die Voraussetzungen des Satzes von Peano erfüllt sind.
b) Zeigen Sie, dass die Funktion f im Punkt (0, 0) nicht lokal Lipschitz-stetig bezüglich y ist.
c) Gegen welche Lösung konvergiert das Polygonzugverfahren?
d) Weisen Sie nach, dass die Lösung des Anfangswertproblems nicht eindeutig ist, indem Sie mindestens zwei verschiedene Lösungen angeben.
könnte mir jemand helfen bitte?
Vielen Dank im Voraus! :)