Symmetrie von Kurvendiskussion

Question

Aufgabe:

Hallo, wie kann ich die Symmetrie dieser Funktion rechnerisch bestimmen?

----> \( \frac{1}{2} \)^4  -2x^3 +4x

:)

Answer 1

Aloha :)

Wenn ein Polynom nur gerade Exponenten hat, ist die Funktion achsensymmetrisch zur y-Achse, denn dann gilt \(f(-x)=f(x)\). Wenn ein Polynom nur ungerade Exponenten hat, ist die Funktion punktsymmetsich zum Ursprung, denn dann gilt \(f(-x)=-f(x)\).

Deine Funktion hat sowohl gerade als auch ungerade Exponenten, daher liegt keine solche Symmetrie vor.

Noch zur Ergänzung, eine Konstate wie z.B. die \(3\) in \(f(x)=x^2+3\) hat einen "geraden" Exponenten, denn \(3=3\cdot x^0\).

Comments

dankeschön :)

---

Schau mal bitte, ich hatte noch was wichtiges vergessen. Das habe ich noch ergänzt ;)

Answer 2

Achsensymmetrie zur y-Achse: f(-x) = f(x)

Punktsymmetrie zum Ursprung: f(-x) = -f(x)

Im Falle

        \(f(x) = \frac{1}{2}x^4 - 2x^3 + 4x\)

ist

        \(f(1) = \frac{5}{2}\qquad f(-1) = -\frac{3}{2}\)

also ist \(f\) weder achsensymmetrisch zur y-Achse, noch punktsymmetrisch zum Ursprung.

Comments

Muss ich hier immer -1 und 1 bei x in der Funktion einsetzen, um zu beweisen,ob es punkt oder -achsensymmetrisch ist?

---

Damit kann man überhaupt nicht beweisen, dass es punkt- oder achsensymmetrisch ist.

Damit kann man beweisen, dass es weder punkt-, noch achsensymmetrisch ist. Dazu kannst du irgend eine Zahl und ihre Gegenzahl einsetzen, nicht nur 1 und -1.

Answer 3

Symmetrie zu x=1

f(x) = 1/2x^4-2x^3+4x

f´(x)=2x^3-6x^2+4

x^3-3x^2+2=0

Bei x=1  gibt es eine Nullstelle, somit ist bei x=1 ein Extremwert

Art des Extremum:

f´´(x)  =  6 x^2-12 x

f´´(1)  =  6 -12 =  - 6  <  0→Maximum

Polynomdivision:

(x^3-3x^2+2):(x-1)=x^2-2x-2

x^2-2x-2=0

x_1=  1 - \( \sqrt[2]{3} \)→y_1=2

x_2=  1 +\( \sqrt[2]{3} \)→y_2=2

f´´(x_1)  → Minimum

f´´(x_2)  → Minimum

Da nun die beiden Minima symmetrisch zueinander liegen und bei x=1 ein Maximum liegt, ist f(x) symmetrisch zu x=1.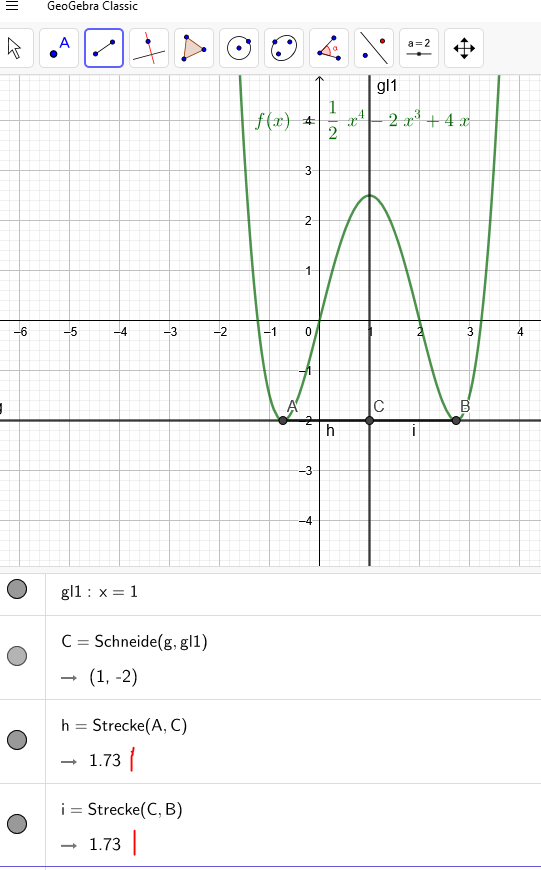

Text erkannt:

GeoGebra Classic
\( \mathrm{g} \mid 1: \times=1 \)
\( \mathrm{C}= \) Schneide \( (\mathrm{g}, \mathrm{g} \mid 1) \)
\( \rightarrow(1,-2) \)
\( h=\operatorname{Strecke}(A, C) \)
\( \rightarrow 1.73 \)
\( \mathrm{i}=\operatorname{Strecke}(\mathrm{C}, \mathrm{B}) \)
\( \rightarrow \)

mfG

Moliets