Hallo,
um ein Optimum zu bestimmen, so leite die Funktion nach \(x_1\) und \(x_2\) ab und setze die Ableitung zu \(0\):$$f\left(x_{1}, x_{2}\right)=-7 x_{1}^{2}+3 x_{1} x_{2}-2 x_{2}^{2}-57 x_{1}+29 x_{2}+15 \\ f_{x1}' = -14x_1 + 3x_2 - 57 = 0\\ f_{x2}' = 3x_1 -4x_2 + 29 = 0$$das ist LGS mit zwei Unbekannten. Die Lösung ist \((x_1;\,x_2) = (-3;\,5)\).
Nun muss man noch prüfen, ob es sich auch um ein globales Optimum handelt. Ok - wenn man weiß, dass es sich um einen nach unten geöffnet (und gestauchten) Paraboloiden handelt ..
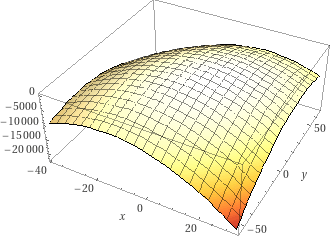
... kann es gar nicht anders sein. Das gesuchte \(x_1\) hat also im Optimum den Wert \(x_1=-3\)