Symmetrie oder nicht? f(x)=2x^5 -4x^3+2x+7

Question

Also meine Lehrerin hat was an die Tafel geschrieben  und ich konnte damit nichts wirklich anfangen .

Und sie konnte mir da auch nicht weiterhelfen .... warum auch immer ... Sie meinte das ist halt so .

Vl könnt hier mir helfen.

Sie schrieb :

f(x)=2x⁵ -4x³+2x+7

-> Keine Symmetrie da es gerade und ungerade Exponenten gibt

 

Aber ich sehe da nur ungerade Exponenten QwQ

Answer 1

Hi,

Da ist ein gerader Exponent versteckt ;).

7 = 7x^0

(x^0 = 1)

Und damit gibt es in der Tat keine Symmetrie zum Ursprung. Allerdings gibt es Punktsymmetrie zu P(0|7).

Da der Graph ja nur nach oben verschoben ist und sonst (wie Du schon gesagt hattest) nur ungerade Exponenten hast ;).

Grüße

Comments

Noch ein Beweisfoto ;).

 

 

Alles klar? :)

P.S.: Die Punktsymmetrie ist in der Schule meist nur bzgl dem Ursprung relevant. Für Schüler wird es hier also wohl keine Symmmetrie geben.

Answer 2

 

f(x) = 2x⁵ - 4x³ + 2x + 7

ist (da x⁰ = 1) gleichbedeutend mit

f(x) = 2x⁵ - 4x³ + 2x + 7x⁰

und da haben wir plötzlich einen geraden Exponenten.

 

Wir haben natürlich keine Achsensymmetrie vorliegen, da dazu alle Exponenten gerade sein müssten, aber auch keine Punktsymmetrie zum Ursprung, weil uns die +7 diese zunichte macht. Hieße die Funktion f(x) = 2x⁵ - 4x³ + 2x, dann hätten wir eine Punktsymmetrie zum Ursprung, aber so ist die Funktion lediglich punktsymmetrisch zu (0|7): 

 

 

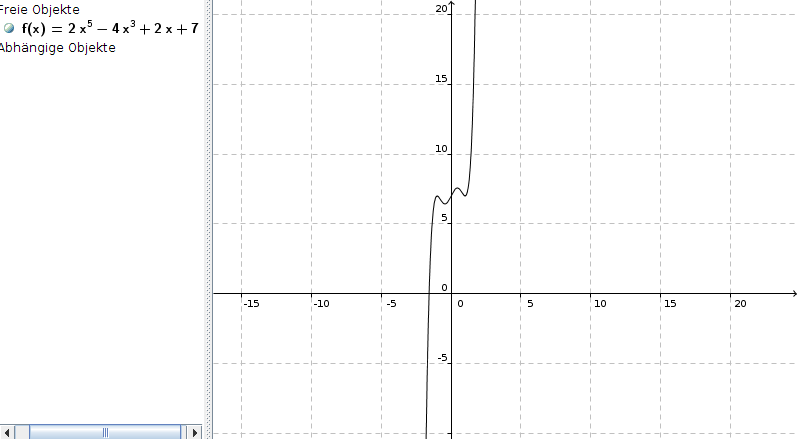
Besten Gruß