Parameterdarstellung für Teilstücke einer Ebene

Question

Aufgabe:

… Von einem Würfel der kantenlänge vier wird eine Ecke abgeschnitten.

A geben Sie eine Parametergleichung für die Ebene an, in der die Schnittfläche liegt

B welche Einschränkungen sind für die Parameter w und u vorzunehmen, damit die Gleichung die dreieckige Schnittfläche beschreibt

Problem/Ansatz:

… dabei geht es um die Parameterdarstellung für Teilstücke eine Ebene.

ich habe eine Skizze bei der die Grundfläche mit einer 2! Dargestellt ist jedoch weiß ich nicht was mir das sagen will

Comments

Wir können nicht hellsehen. Wir wissen nicht, wie dein Würfel im Koordinatensystem liegt und welche die weggeschnittene Ecke ist. Wir kennen nicht die Koordinaten der drei Eckpunkte deiner Schnittfläche.

---

Darf man Fotos von Arbeitsblättern hier einfügen oder weder Buchseiten noch Arbeitsblätter?

---

Wie lange würde es denn dauern, wenn du mit einem Bleistift und einem Blatt Papier die Ansicht skizzierst?

Answer 1

Das könnte man sich eventuell wie folgt vorstellen

https://www.matheretter.de/geoservant/de?draw=quader(-2%7C-2%7C-2%204%7C4%7C4)%0Aebene(2%7C0%7C2%202%7C2%7C0%200%7C2%7C2)

Ob es tatsächlich so aussieht, kannst nur du wissen.

Answer 2

Hallo Leonie,

Im Bild siehst Du einen Würfel, von dem eine Ecke abgeschnitten wurde:

Ich habe den Würfel mit der Kantenlänge \(l=4\) mit einer Ecke in den Koordinatenursprung gestellt. Die Längen der Kanten, die nach dem Abschneiden stehen geblieben sind, habe ich mit \(a=3\), \(b=2\) und \(c=1\) bezeichnet. Die Werte sind frei gewählt. Einen der Schnittpunkte (hier \(P\)) der Schnittebene mit den Würfelkanten wählt man als Stützpunkt für die Ebene in Parameterdarstellung. Die Richtungsvektoren \(\vec r\) (grün) und \(\vec s\) (blau) sind dann die Differenzen der verbleibenden Schnittpunkte zu \(P\).

Allgemein gilt hier:$$\begin{aligned} E: \quad \vec x &= P + w \vec r + u \vec s \\&= \begin{pmatrix}l\\ l\\ c\end{pmatrix} + w \begin{pmatrix}a-l\\ 0\\ l-c\end{pmatrix} + u \begin{pmatrix}0\\ b-l\\ l-c\end{pmatrix} \\ &= \begin{pmatrix}4\\ 4\\ 1\end{pmatrix} + w \begin{pmatrix}-1\\ 0\\ 3\end{pmatrix} + u \begin{pmatrix}0\\ -2\\ 3\end{pmatrix}\end{aligned}$$

welche Einschränkungen sind für die Parameter w und u vorzunehmen, damit die Gleichung die dreieckige Schnittfläche beschreibt

Die Einschränkungen sind: $$\begin{aligned} w &\ge 0 \\ u &\ge 0 \\ w+u &\le 1 \end{aligned}$$Falls Dir etwas unklar ist, frage bitte nach.

(Wenn Du auf das Bild klickst, kannst Du die Szene mit der Maus drehen und bekommst einen besseren räumlichen Eindruck)

Comments

Hallo,

ich bin gerade an einer ähnlichen Aufgabe. Die Parameterdarstellung war kein Problem.

Ich frage mich, warum die Einschränkungen für die Parameter so sind.

Idee:

Falls s und t nicht größer als 0 sind, erhalten wir zum Beispiel x1 und x2 Koordinaten, die größer als 4 und somit außerhalb des Würfels liegen.

Und s+t=1, da ansonsten die x3-Koordinaten größer als 4 wäre.

Was mich dabei verwirrt: Könnte der Punkt nicht trotzdem in der Ebene liegen, auch wenn zum Beispiel die Werte der Koordinaten größer als 4 sind, weil man Punkte ja nicht genau ablesen kann und durch die kombinierte Verschiebung der Punkt evtl. doch in der Ebene ist. Für Denkanstöße wäre ich dankbar!

---

Hallo,

Und s+t=1, da ansonsten die x3-Koordinaten größer als 4 wäre.

weil bei größeren Werten die \(x_3\)-Koordinate größer als 4 würde - das ist hier in diesem speziellen Fall richtig. Aber trenne Dich mal von den \(x_1,x_2,x_3\)-Koordinaten. Diese Einschränkung gilt für jedes(!) Dreieck welches von zwei Vektoren aufgespannt wird.

Dazu folgendes Bild:

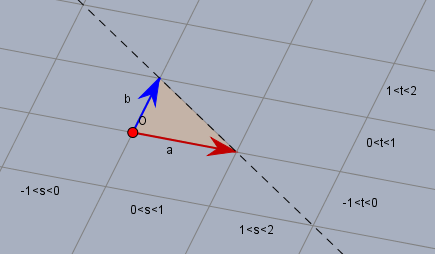
Das ist ein Gitter mit parallelen und äquidistanten Geraden. Die Gitterliniene müssen nicht senkrecht auf einander stehen, noch müssen die Abstände in der einen mit den Abstaänden der anderen Richtung überein stimmen.

Mit anderen Worten: man kann dieses Gitter mit zwei beliebigen (linear unabhängigen) Vektoren \(\vec a\) und \(\vec b\) definieren. Jeder Punkt \(\vec p\) auf der Ebene lässt sich nun durch eine Linearkombination von \(\vec a\) und \(\vec b\) beschreiben:$$\vec p = s\vec a + t\vec b $$sind \(s\) und \(t\) ganze Zahlen landet man mit \(\vec p\) immer auf einem Gitterpunkt. Ist \(s<0\) so liegt \(\vec p\) immer links von der Gearden auf der das (blaue) \(\vec b\) liegt. Ist \(s>0\) so liegt \(\vec p\) rechts davon. Ist \(t>0\) liegt \(\vec p\) oberhalb der Geraden, auf der der (rote) Vektor \(\vec a\) liegt.

Wo liegen alle Punkte für die \(s>0\) und \(t>0\) gilt?

Nun überlege mal, wie man die gestrichelte Gerade beschreiben soll! Starte bei $$\vec p_0 = \vec b$$die Richtung der Geraden ist \(\vec a - \vec b\) - also kann man diese Gerade in Parameterform schreiben:$$g: \quad \vec x = \vec p_0 + \lambda(\vec a - \vec b) = \vec b + \lambda(\vec a - \vec b) = \lambda\vec a +(1-\lambda) \vec b$$Nehme nun wieder einen beliebigen Punkt $$\vec p = s\vec a + t\vec b$$was kannst Du zu \(s+t\) sagen, wenn \(\vec p\) auf \(g\) liegen soll?

Gruß Werner

---

Vielen, vielen Dank! Jetzt verstehe ich auch die Einschränkung für s+t.