Aus x(p) = 140 - 0,2p (das ist Menge in Abhängigkeit vom Preis) folgt durch Umformung
Preis p = 5*(140-x) (das ist der erzielbare Preis wenn man x Stück verkaufen will)
Der Erlös ist p * x = 5*(140-x) * x = -5x2 + 700x.
Die Erlösfunktion (rot) und die Kostenfunktion (blau) verhalten sich also so:
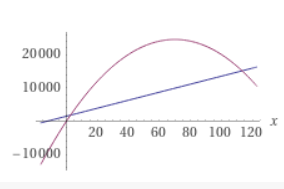
Die Gewinnfunktion ist die Differenz davon, im Bild grün:
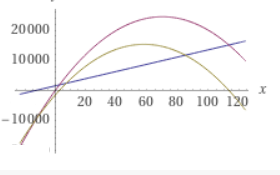
Die Gewinngrenze erhält man durch Kosten = Erlös (zwei Lösungen).
Das Gewinnmaximum erhält man, indem man die erste Ableitung der Gewinnfunktion gleich Null setzt und sie löst, ich komme auf x = 58.
Die Stückzahl, bei der mindestens 10000 Euro Gewinn erzielt werden, erhält man indem man die Gewinnfunktion gleich 10000 setzt und diese quadratische Gleichung löst. Ich komme auf eine untere Grenze von etwa 25.4 Stück (darunter ist die Menge zu klein) und eine obere Grenze von etwa 90.6 Stück (darüber ist der erzielbare Preis zu klein), wobei man das runden soll weil es nur ganze Fahrräder gibt.