Aufgabe: Masse eines Kegelstumpfs berechnen
Wir betrachten in den Fragen auf dieser Seite einen Kegelstumpf mit inhomoger Dichteverteilung in dimensionsbehafteten Größen (SI-Einheiten).
Die Grundfläche des Kegelstumpfs hat den Radius r _1 = 0,02 m und liegt in der x-yEbene. Die obere Fläche liegt in einer Höhe ℎ = 0,024 m über der Grundfläche und hat einen Radius r_2 = 0,01 m.

Die Dichteverteilung in diesem Kegelstumpf ist durch die Funktion
rho(r )=1,8 kg/cm^3 + 1,3 kg/cm^4 +( 0,6 kg/cm^5)*z^2
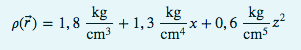
Text erkannt:
\( \rho(\vec{r})=1,8 \frac{\mathrm{kg}}{\mathrm{cm}^{3}}+1,3 \frac{\mathrm{kg}}{\mathrm{cm}^{4}} x+0,6 \frac{\mathrm{kg}}{\mathrm{cm}^{5}} z^{2} \)
gegeben.
Berechnen Sie nun zunächst die Masse M des Kegelstumpfs und wählen Sie die richtige Antwort (geg. in Kilogramm (kg)) aus!
1. 41,0
2. 50,1
3. 31,9
4. 45,6
5. 36,5
Problem/Ansatz:
Ich habe leider keine Ahnung, wie ich an dieses Problem herangehen soll. Wäre super, wenn mir jemand helfen könnte :)