Bedeutet "Wenn A, ... dann B?" das Gleiche wie "Wenn A eintritt, dann B", das Gleiche wie "Wenn A wahr ist, ... dann...?

Question

Liebe Lounge, frohes Neues!

Ich plage mich mit der Formulierung "Wenn, ..., dann...".

Also mit der Verbalisierung einer Implikation.

Häufig liest man: "Wenn A eintritt, dann tritt B ein". Das soll stehen für A⇒B.

Jetzt  habe ich eine Frage zur Formulierung: "Wenn A eintritt" bedeutet nicht "Wenn A wahr ist" oder?

Weil ansonsten würde für mich die Wahrheitstafel der Implikation keinen Sinn ergeben...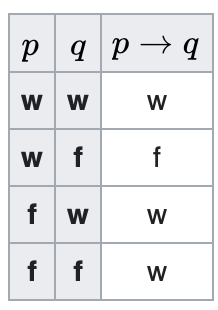

Auf der anderen Seite würde das aber auch bedeuten: A kann auch eintreten, wenn es nicht wahr ist.

Ich bin verwirrt.

Was wäre dann z.B. mit A: 2+4=9  und B: 2+4=6

Würde man jetzt hier formulieren: Wenn 2+4=9 ergibt, dann ist 2+4=6 ?

In der Formulierung steckt ja irgendwie schon drin: Wenn 2+4=9 wahr ist, dann ...

Nun ist es ja da offensichtlich, dass A nie wahr ist. Kann es dann überhaupt eintreten? Sprich: Vorausgesetzt 2+4=9 wäre wahr, dann ist 2+4=6.

Danke euch, schönen 1.

Answer 1

Du kannst A → B auch lesen als wenn A wahr ist, dann ist auch B wahr.

Ob man jetzt eintritt oder wahr sagt, spielt keine Rolle.

A kann also nicht eintreten wenn A falsch ist weil eben eintreten und wahr das Gleiche ist.

Würde man jetzt hier formulieren: Wenn 2+4=9 ergibt, dann ist 2+4=6 ?

Ja das ist richtig. Und da 2 + 4 = 9 eine falsche Aussage ist kann daraus über die Richtigkeit der anderen Aussage nichts abgeleitet werden.

Comments

Lieber Coach,

Ja das ist richtig. Und da 2 + 4 = 9 eine falsche Aussage ist kann daraus über die Richtigkeit der anderen Aussage nichts abgeleitet werden.

Man würde aber hier jetzt dennoch sagen, dass A⇒B wahr ist...

Oder liege ich da falsch? Und das verstehe ich nicht...

---

vgl:

https://de.wikipedia.org/wiki/Ex_falso_quodlibet

---

Nein. A → B bedeutet, dass es zwangsläufig folgt das aus A B folgt.

A: Ich huste
B: Ich habe Corona

Gilt jetzt A → B nur, wenn ich zufällig huste und Corona habe?

Ich könnte auch husten, ohne Corona zu haben.

Die Wahrheitstabelle bei dir muss also für jede Aussage von p und q erfällt sein damit diese Implikation gilt.

Nimm meinetwegen das typische Beispiel

A: Es regnet
B: Die Straße ist nass

---

Also "gilt" eine Implikation nur genau dann, wenn sie auf jeden Fall auch wahr ist!?

---

Ja. Wenn, sie für jede Aussage von A und B auch wahr ist.

Wenn es regnet dann ist die Straße nass.

Es gibt zwei Fälle.

1. Es regnet. Dann muss in jedem Fall die Straße nass sein, damit A → B wahr ist, ansonsten ist A → b falsch

2. Es regnet nicht. Hier kann keine Aussage über die Straße gemacht werden. Die Straße kann also sowohl trocken als auch nass sein.

---

Aber für 2. wäre doch laut der Wahrheitstabelle A--> B wahr ? :(

---

Aber für 2. wäre doch laut der Wahrheitstabelle A--> B wahr ? :(

Ja genau. Eben weil keine Schlussfolgerung gegeben ist.

A → B kannst du auch übersetzen mit "nicht A oder B"

---

Sprich Schlussfolgerung bezieht sich immer auf die gesamte Implikation. Also ob diese sicher wahr ist.

Und diese ist nicht sicher wahr, wenn nicht alle Möglichkeiten zu einer wahren Implikation führen ?

---

Hallo coach,
kleiner Hinweis : k ist ein Troll.
mfg Georg

---

Und diese ist nicht sicher wahr, wenn nicht alle Möglichkeiten zu einer wahren Implikation führen ?

Sprichst du jetzt von der nassen Straße? Doch das wäre eine wahre Implikation.

Wenn es Regnet ist die Straße mit Sicherheit nass und nicht trocken.

Damit ist die Implikation wahr.

---

Georg , was soll das?

Ich dachte, dass die Lounge ein Forum ist, bei welchen Leuten geholfen wird.

Und ich würde ja nicht fragen, wenn ich es verstanden hätten.

Und wenn du nicht helfen willst, dann lass es eben. Aber halte doch nicht andere Leute davon ab zu helfen ?

Und mir waren deine Ausführungen nicht klar ..

---

Vielleicht schaust du dir auch noch andere Quellen und Beispiele an.

https://de.wikipedia.org/wiki/Implikation

---

Habe es glaube verstanden, danke!

Die Frage die sich mir stellt ist:

Warum betrachtet man die Wahrheitstafel überhaupt für Fälle bei denen A nicht wahr ist?

Das ist doch eigentlich nicht interessant oder?

---

Das ist nicht uninteressant weil für die Fälle die Implikation ja immer wahr ist.

Man berücksichtigt in einer Wahrheitstabelle immer alle Möglichkeiten die auftreten können.

---

Ok. Nur nochmal zum Verständnis:

A: Rom liegt in Deutschland B: 2 ist ungerade

A—> B währe Aussagenlogisch wahr?

A ist offensichtlich falsch. Deshalb folgt die Implikation.

Demnach schaut man sich den Fall, dass A wahr wäre nicht an, da nicht möglich.

---

Die Aussagenlogik macht doch eigentlich nur sinn wenn A und B Platzhalter sind für Aussagen die Wahr oder Falsch sein können. Und nicht nur Für Aussagen die einen bestimmten Wahrheitswert annehmen.

Es ist natürlich richtig, dass die Implikation wahr ist. Aber dann braucht man das auch nicht als Implikation aufschreiben.

Wenn du weißt das 1 + 1 = 2 ergibt dann schreibst du ja auch 1 + 1 in der Regel nicht als Rechnung auf. Es sei denn du willst irgendeinen Fall verdeutlichen.

Also folgende Implikationen sind wahr.

Falsch → Falsch
Falsch → Wahr
Wahr → Wahr
Aber dann brauch ich das auch nicht aufschreiben.

---

Du meinst, wenn A und B sowohl wahr UND falsch sein können. Und es nicht von vornherein klar ist, dass eine der Aussagen auf jeden Fall wahr oder falsch ist ?

Das heißt (obwohl ich das schonmal gefragt habe):

Wenn ich folgenden Satz beweisen will:

Sei n eine Natürliche Zahl, dann ist (n+(n+1)+(n+2)/3 wieder eine natürliche Zahl.

Hier interessiert mich doch eingebrochen nur der Fall, in dem A wahr ist oder? Weil ich mich ja frage, ob das stimmt, wenn n eine natürliche Zahl ist.

Demnach würde ich da die Fälle, dass A falsch ist, nicht Betrachten (da damit die Implikation ohnehin richtig wäre)

---

Richtig. Das Problem reduziert sich eigentlich nur auf die Überprüfung ob (n+(n+1)+(n+2)/3 eine natürliche Zahl ist.

Bei einer allgemeinen Implikation A → B weißt du aber in der Regel nicht ob A wahr oder falsch ist.

Und eigentlich behandelt man in der Aussagenlogik auch nur Aussagen die wahr oder falsch sein können.

Weil wenn ich eben weiß ob eine Aussage wahr oder falsch ist dann lassen sich aussagenlogische Formeln ohnehin vereinfachen.

Wir haben gasagt

A → B ist das gleiche wie nicht A oder B

Wenn ich nun aber weiß das A wahr ist dann ist

wahr → B ist das gleiche wie nicht wahr oder B = falsch oder B = B

Also Fragt man dann nur ob B wahr oder falsch ist. Dann ist das auch unsinnig das als Implikation aufzuschreiben.

---

Aber dann dürfte doch die allgemeine Implikation A—> B verbalisiert auch nicht bedeuten:

Wenn A WAHR ist, dann ist B wahr?

Weil das schließt ja sozusagen die Fälle aus, dass A falsch ist...

---

Wenn du es untersuchst brauchst du auch nur zeigen das wenn A gilt, dass dann auch B gilt.

Alles andere interessiert dich nicht um die Wahrheit einer Implikation zu bewerten.

---

Okay. Meine allerletzte Frage, dann gebe ich Ruhe:

Voraussetzung: n ist Natürliche Zahl

Behauptung: (3n+3)/3 ist natürliche Zahl

Den Beweis führe ich in der Regel ja ohne überhaupt an eine Wahrheitstafel zu denken.

---

Den Beweis führe ich in der Regel ja ohne überhaupt an eine Wahrheitstafel zu denken.

Richtig. Du sollst ja auch nur prüfen ob (3n+3)/3 = n + 1 eine natürliche Zahl ist. Und das ist sicher der Fall wenn n eine natürliche Zahl ist.

---

Dann wünsche ich dir jetzt einen schönen Abend!