ich komme so gar nicht weiter bei den Aufgaben. Ich habe nach jeder Teilaufgabe die Lösung die ich als richtig empfand dahinter geschrieben. Mein Ansatz war wie folgt. VIELEN LIEBEN DANK ❤️
Aufgabe: Lassen Sie uns annehmen, dass Ihr persönliches Glück y unter anderem von zwei Produkten abhängt. Zum einer von der Menge eines von Ihnen mit Vorliebe konsumierten Getränks x1 und zum anderen von der Anzahl der mit einer geschätzten Person verbrachten Zeit x2. Zur Berechnung des Gesamtglücks kann man dieses nun in verschiedene Teilglücke yi zerlegen und die Teilglücke dann zum Gesamtglück additiv verknüpfen. Der Glücksbeitrag y1 von x1 kann durch eine der folgenden Funktionen beschrieben werden:
- y1a(x1) = −0.05x1^3 + ax1^2 + 0.1x1
- y1b(x1) = a√x1
- y1c(x1) = ax1^2
wobei a > 0 sei.
Die Graphen der Funktionen sehen wie folgt aus:
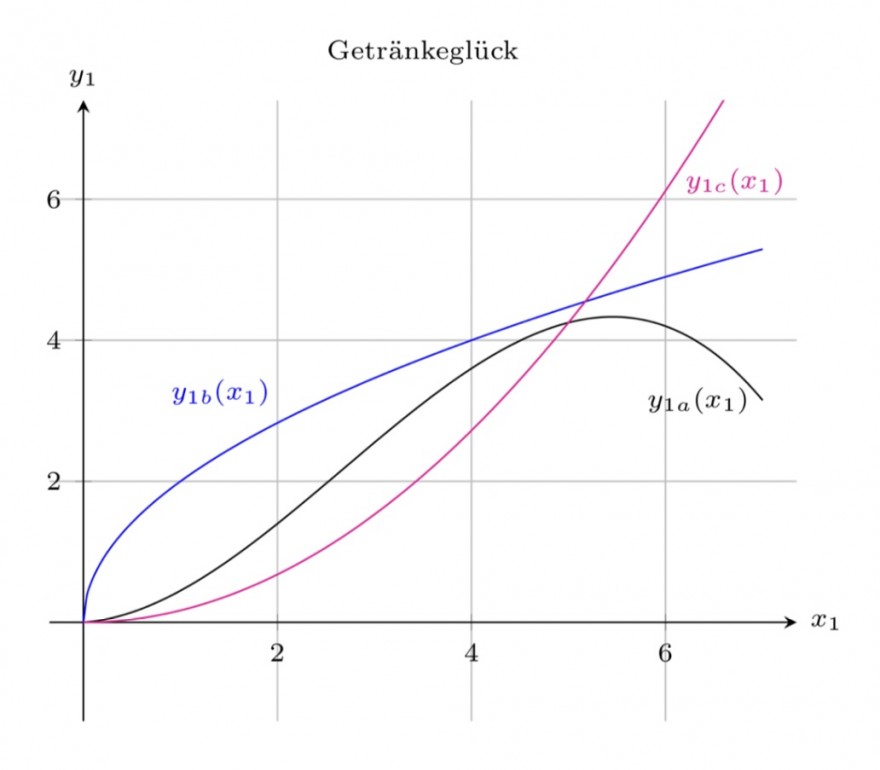
Der Glücksbeitrag von x2 sei linear angenommen:
y2 = y2(x2) = 1.2x2
Zudem kann man denke ich berechtigter Weise annehmen, dass ein Getränk in Gemeinschaft besser schmeckt und ergo glücklicher macht. Andererseits gibt es ja auch die Theorie, dass die mit einer Person verbrachte Zeit durch den Konsum gewisser Getränke (noch) schöner wird. Somit gibt es einen sich gegenseitig verstärkenden Einfluss, den wir mal als mittels des Terms:
y3=y(x1,x2)=0.2x1^0,4 x2^0,6
beschrieben annehmen. Wie oben beschrieben ergebe sich das Gesamtglück y additiv: y(x1, x2) = y1 + y2 + y3
Beziehen Sie sich bei den folgenden Aufgaben nur auf die Funktion y1(x1):
a) Entscheiden Sie, welche der drei y1-Funktionen den Glücksbeitrag des Getränkes Ihrer Meinung nach am besten abbildet. Begründen Sie Ihre Entscheidung.
A: Habe mich für y1a entschieden Begründung habe ich auch.
b) Wählen Sie dann für die Konstante a der von Ihnen als passend angenommenen Funktion einen Wert im folgenden Intervall:
- Funktion y1a : a ∈ [0.35; 0.45]
- Funktion y1b : a ∈ [1.5; 2.5]
- Funktion y1c : a ∈ [0.10; 0.17]
A: Wert in die Funktion y1a, 0,35 einsetzen für a. und dann ?
c) Bestimmen Sie für eine von Ihnen im Intervall zwischen x1 = 1 und x1 = 5 gewählte, derzeit konsumierte Menge des Getränkes den Glücksbeitrag eines weiteren kleinen Schlucks.
A: Für einen Schluck nehme ich als Annahme den Wert 0,1 als Steigung, welches die Veränderung darstellt. Für x1 nehme ich den Wert 3 und setze den dann in die erste Ableitung die ich jetzt bilde ein. y´1a= 0,15x^2+a3x1^2+a2x1+0,1. Dann setze ich für x=3 ein und für a=0,35 und erhalte als konsumierte Menge= 13
d) Wird der Glücksbeitrag weiterer kleiner Schlücke größer oder kleiner ausfallen als der des Schlucks in c)? Begründen Sie Ihr Antwort mathematisch.
A: Zweite Ableitung wird gebildet y´´1a= -0,3x1+6ax1+2a. Dann wieder für x 3 einsetzten für a 0,35. Der Glücksbeitrag ist 6,1, also weniger geworden.
Beziehen Sie sich bei der folgenden Aufgabe nur auf die Funktion y3(x1; x2):
e) Zeigen Sie, dass die Funktion für den Fall, dass sowohl vom Getränk konsumiert wird als auch die geschätzte Person getroffen wird (d. h. x1 > 0 und x2 > 0), kein Maximum besitzt.
A: Muss man hier Extremwerte berechnen? Mit oder ohne Nebenbedingung? y3 = y3(x1, x2) = 0.2x1^0.4 x2^0.6 Für x1/x2=3 aus Aufgabe c einsetzten dann erhält man: 0,31>0 und 1,933>0
Beziehen Sie sich bei den folgenden Aufgaben auf die Funktion y(x1; x2):
f) Wie groß ist der Glücksbeitrag eines weiteren kleinen Schlucks bei der von Ihnen unter c) gewählten, derzeit konsumierten Menge des Getränks, wenn Sie derzeit 2 Zeiteinheiten x2 mit der von Ihnen geschätzten Person verbringen?
A: 0,1 ein Schluck, für x2 2 einsetzen. Für x1 aus c die 3 und für a 0,35 wieder einsetzen. Alle drei Funktionen zusammen addieren und dann erhält mann: y1= 11,55; y2= 2,4; y3= 1,83 Insgesamt= 15,78
g) Wie würde sich der Glücksbeitrag des kleinen Schlucks verändern, wenn Sie ceteris paribus etwas mehr Zeit mit der Person verbringen könnten?
A: Je mehr Zeit desto langsamer steigt das Glück an?
h) Welche Information würde Ihnen die erste Ableitung der Isoglücksfunktion geben?
A: Zeigt die Steigung des Glückbeitrags an? Je länger ich mit der Person Zeit verbringe, desto glücklicher aber hintenraus ist das Glück irgendwann aufgebraucht?