Hallo,
Eine Zeichnung hilft immer weiter:
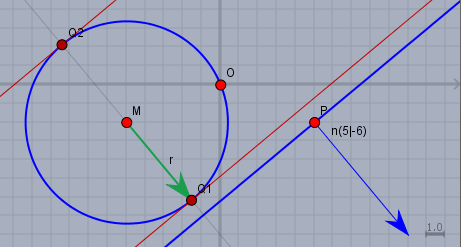
Der Kreis hat seinen Mittelpunkt bei \(M(-5|\,-2)\) und den Radius von \(\sqrt{29}\). Der Punkt \(P(5|\, -2)\) erfüllt die Geradengleichung und liegt somit auf \(g\) und der Normalenvektor \(\vec n\) der Geraden \(g\) ist$$\vec n = \begin{pmatrix}5\\ -6\end{pmatrix}$$Wie kommt man nun zu den Berührpunkten \(Q_{1,2}\) der Tangenten \(t_{1,2}\)? Indem man vom Mittelpunkt \(M\) aus einmal in Richtung und einmal in Gegenrichtung von \(\vec n\) läuft (der grüne Pfeil). Und in jedem Fall so weit, wie der Radius des Kreises ist. Folglich ist$$Q_{1,2} = M \pm \frac{\vec n}{|\vec n|} \cdot \sqrt{29} = \begin{pmatrix}-5\\ -2\end{pmatrix} \pm \sqrt{\frac{29}{61}} \begin{pmatrix}5\\ -6\end{pmatrix}$$und daraus kann man unmittelbar die Normalen- (bzw. Koordinaten-)Gleichung der gesuchten Tangenten aufstellen:$$t_{1,2}: \quad 5x - 6y = -13 \pm \sqrt{29 \cdot 61}$$Falls Du dazu Fragen hast, so melde Dich bitte.
Gruß Werner