f (x) = - 0,24 x^2 + 12x
a) Berechne die Höhe des Feuerwerkskörpers bei einer horizontalen Entfernung von 10m vom Abschussort.
f (10) = - 0,24 *10^2 + 12*10=96
b) die allgemeine Gleichung in die Scheitelpunktform überführen
y = - 0,24 x^2 + 12x|:(- 0,24 )
\( \frac{y}{-0,24} \) = x^2 - 50x|+625
\( \frac{y}{-0,24} \)+ 625 = x^2 - 50x+625
\( \frac{y}{-0,24} \)+ 625 = (x-25)^2| -625
\( \frac{y}{-0,24} \) = (x-25)^2 - 625|*(-0,24)
y = - 0,24(x-25)^2+150
c) Nullstellen:
- 0,24 x^2 + 12x=0
x*(-0,24 x+12)=0
x₁ = 0
(-0,24 x+12)=0
x₂ = 50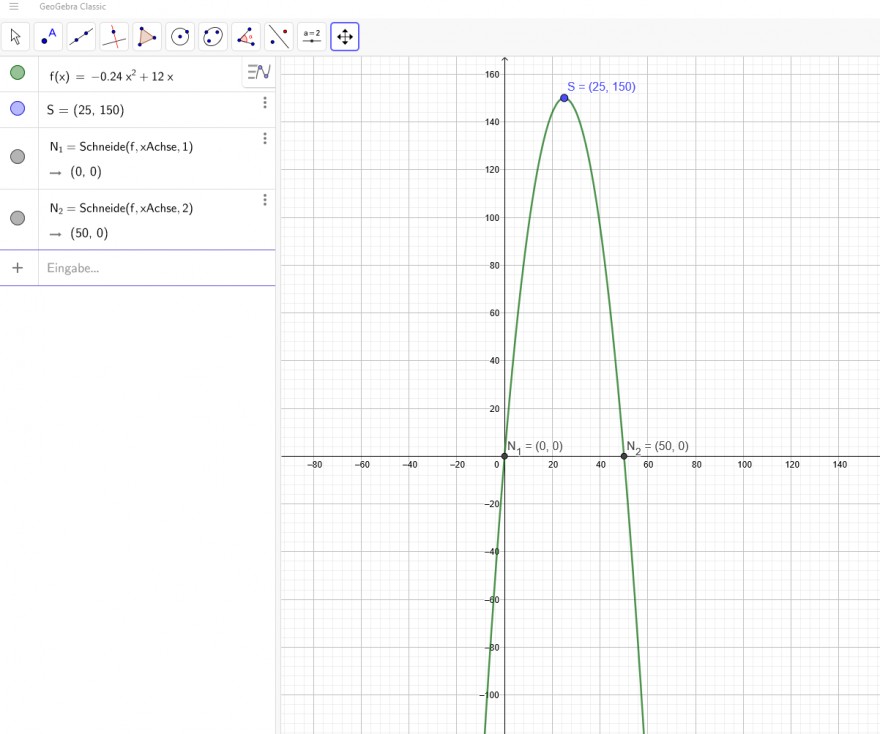
Text erkannt:
GeoGebra Classic
\( f(x)=-0.24 x^{2}+12 x \)
\( =N \)
\( S=(25,150) \)
\( \mathrm{N}_{1}= \) Schneide( \( \mathrm{f}, \) xAchse, 1 )
\( \rightarrow(0,0) \)
\( \mathrm{N}_{2}= \) Schneide \( (\mathrm{f}, \) xAchse, 2 )
\( \rightarrow(50,0) \)