Text erkannt:
\( f(x)=\frac{1}{8} x^{4}-\frac{3}{4} x^{2}+ \)
\( A= \) Schneide(f, xáchse, 2 ) \( \rightarrow(-1,0) \)
\( B=(1,0) \)
g : Tangente(A,f)
ngente(B,f)
\( \alpha= \) Winkel \( (\mathrm{h}, \mathrm{g}) \)
\( +\frac{3}{4} x^{2}-5 \)
: Tangente(A,p)
\( 3, p) \)
\( i, j \)
Funktion vierten Grades, die symmetrisch zur y-Achse ist und einen Wendepunkt bei (1|0) hat. Die beiden Wendetangenten schneiden sich s e n kr e c h t.
f(x)=a*x^4+b*x^2+c
Wendepunkt bei (1|0):
f(1)=a+b+c
1.) a+b+c=0
f ´( x )= 4 a*x^3+2 b*x
f ´´( x ) = 12 a*x^2+2 b
f ´´( 1 ) = 12 a+2 b
12 a+2 b=0
2.) 6 a + b=0->b=(-6a )in 3.)
Die beiden Wendetangenten schneiden sich s e n k r e c h t:
1.Wendepunkt bei (1|0):
f ´( 1 )= 4 a+2 b
2.Wendepunkt bei (-1|0):
f ´ ( -1 )= 4 a*(-1)^3+2 b*(-1)=-4a-2b
4 a+2 b=-1/(-4a-2b)=1/(4a+2b)
4 a+2 b=1/(4a+2b)
3.)(4a+2b)^2=1
(4a+2*(-6a ))^2=1
(-8a)^2=1
a_1=1/8->b_1=(-6*1/8 )=-3/4
a_2=-1/8->b_2=(-6*(-1/8 ))=3/4
1.) 1/8-3/4+c_1=0
c_1=5/8
2.) -1/8+3/4+c_2=0
c_2=-5/8
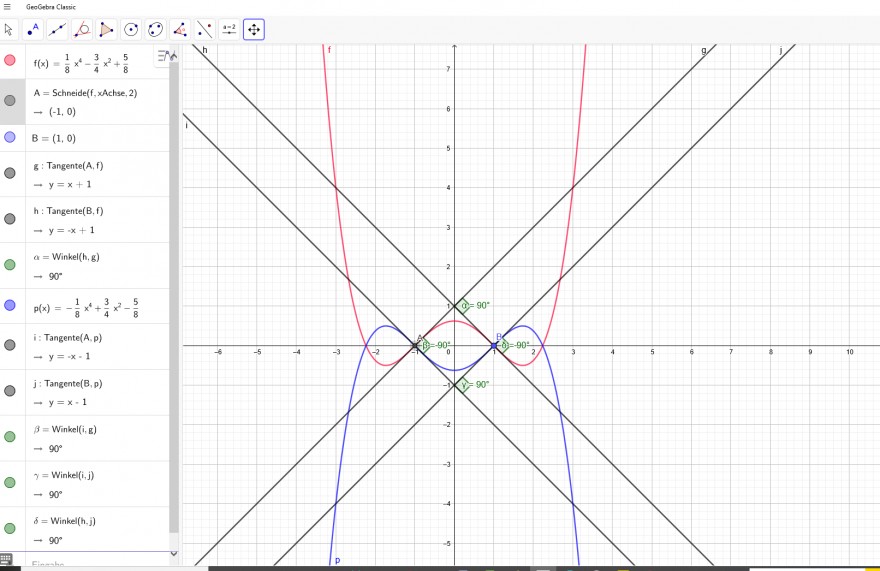
Funktion 1) in r o t
f(x)=1/8*x^4-3/4*x^2+5/8
Funktion 2)in b l a u
g(x)=-1/8*x^4+3/4*x^2-5/8