b) Bestimmen Sie die Breite und die Tiefe des Flusses.
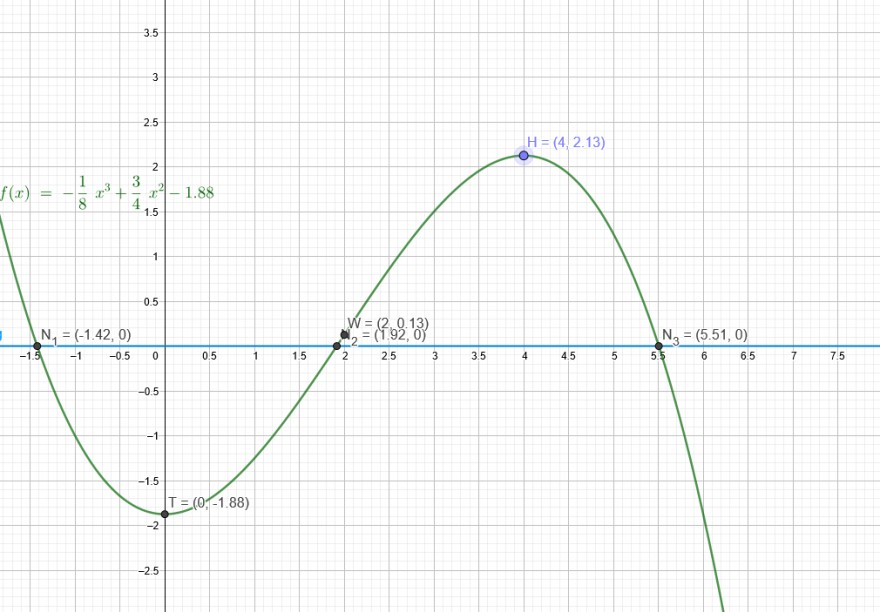
f(x) = - \( \frac{1}{8} \) x^3 + \( \frac{3}{4} \) x^2-1,875
f´(x) = - \( \frac{3}{8} \) x^2 + \( \frac{3}{2} \) x
f´´(x) = - \( \frac{3}{4} \) x + \( \frac{3}{2} \)
f´(x) =0
- \( \frac{3}{8} \) x^2 + \( \frac{3}{2} \) x = 0
x₁ = 0 → f(0) = -1,875
x₂ = 4→ f(4) = 2,125
Art des Extremum
f´´(0) = \( \frac{3}{2} \) >0 → Minimum
f´´(4) = - \( \frac{3}{4} \) *4 + \( \frac{3}{2} \) <0 → Maximum
Wendepunkt:
f´´(x) =0
-\( \frac{3}{4} \) x =\( \frac{3}{2} \)
x= 2 →f(2 )= - \( \frac{1}{8} \) (2)^3 + \( \frac{3}{4} \) *4-1,875= 0,125
Nullstellen:
- \( \frac{1}{8} \) x^3 + \( \frac{3}{4} \) x^2-1,875=0
Ergibt ganz krumme Werte. Benütze ein Näherungsverfahren.
Der Fluss hat eine Tiefe von ... m (→ Minimum) LE beachten
c)...
 mfG
mfG
Moliets