Aufgabe:
Dank Corona können Sie 2021 nicht ans Meer fahren um Urlaub zu machen. Deshalb beschließen Sie einen Wanderurlaub in Österreich zu machen. Das Bergprofil Ihrer Zielregion kann durch die Funktion
$$f: [-\frac{3}{2}, 4]\rightarrow \mathbb{R}, x \rightarrow x^{5} - \frac{65}{12}x^{4} + \frac{45}{2}x^{2} + 25$$
beschrieben werden (siehe Skizze).
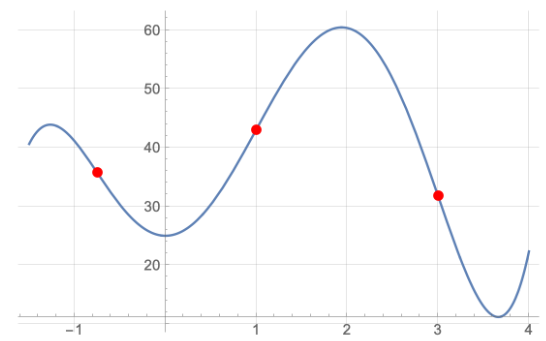
Sie haben es sich zum Ziel gesetzt den steilsten Berg zu bezwingen. Ein Freund aus der Region zeichnet Ihnen die steilste Passage jedes Berges als roten Punkt ein; diese liegen bei x = −3/4, x = 1 und x = 3. Er weiß nur leider nicht mehr, welche von diesen Stellen die insgesamt steilste war. Glücklicherweise wissen sie, dass die Steigung einer Funktion in einem Punkt durch die Steigung der Tangente in diesem Punkt beschrieben wird. Berechnen Sie damit welchen Berg Sie von welcher Seite besteigen müssen, um Ihr Ziel zu erreichen.