Warum hat der Integrand als Differential und als Argument ein t und nicht ein x?

Question

Liebe Lounge,

eine Frage zur Integralfunktion als Bestandteil des HDI.

Man findet als Integralfunktion folgende Definition:

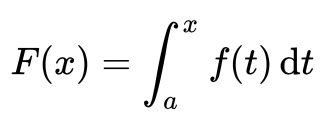
Der Beweis des HDI enthält ja jetzt im Kern, dass F'(x)=f(x).

Warum hat der Integrand als Differential und als Argument ein t und nicht ein x?

Ich meine wahrscheinlich liegt es daran, dass x die Grenze ist, aber so 100%ig verstehen tue ich es nicht. Würde doch theoretisch auch mit f(x)dx gehen - oder?

Answer 1

F hat als Variable die obere Grenze, die sollte nicht dasselbe Symbol verwenden wie der Intergrand. statt t geht jeder andere Buchstabe, ausser x im Integral. .

Gruß lul

Comments

Aber wieso? Also wo entsteht dann ein Problem?

---

Hallo

das Problem entsteht weil du 2 verschiedene Stellen hast, wo x als Variable steht, und völlig verschieden benutzt wird. Das eine x in F(x)  gibt die Änderung des Flächeninhaltes unter einer kurve bis zur Stelle x an. wenn du dasselbe unter dem Integral verwendest beschreibt f(x) den Graph der Kurve. es macht keinen Sinn eine und dieselbe Variable für den Verlauf einer Kurve und den Flächeninhalt zu verwenden.

Etwa du bezeichnest die Seite eines Quadrates mit x und den Flächeninhalt auch. Dass $$\int \limits_{0}^{b}f(x)dx und \int \limits_{0}^{b}f(y)dy und \int \limits_{0}^{b}f(t)dt$$ alle dasselbe F(b) geben ist dir klar.

Auf der Schule schlampen viele L. und deshalb auch SuS weil sie egal was für ne Variable im Integral steht , ohne zu denken einfach integrieren und das Ergebnis ja stimmt.

Gruß lul

---

Also wo entsteht dann ein Problem?

Es entsteht überhaupt kein Problem.

---

Also Lul. Mir ist klar, dass die Integrale die du aufschreibst das gleiche bedeuten.

Aber so richtig wird mit noch nicht klar, warum man da jetzt nicht zwei mal x benutzen kann...

Und @hj2166: das heißt ?

---

Bei Beweis wird ja dann auf einmal aus f(t) auch wieder f(x)... Da ist es dann egal?

---

Hallo

da ich nicht weiss, um welchen Beweis es geht, kann ich dazu nichts sagen. Wenn etwa im Beweis gesagt wird f(x) ist stetig, oder eine andere Eigenschaft, ist das egal wenn f(x) die Eigenschaft hat, dann auch f(z) oder f(t)

und ich sehe auch nicht wo dein Problem noch ist!

lul