Aufgabe:
Nach einer Stichprobe kann die Hypothese H0:p = 0,9 zugunsten von H1:p < 0,9 auf dem 5%-Signifikanzniveau verworfen werden.
für n=10
Annahmebereich [7;10],
Verwerfungsbereich [0;6]
Problem/Ansatz:
Berechnen Sie das 95,4%-Vertrauensintervall
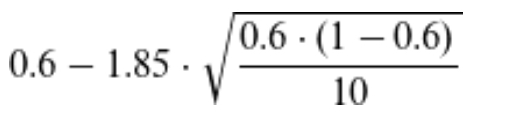
Text erkannt:
\( 0.6-1.85 \cdot \sqrt{\frac{0.6 \cdot(1-0.6)}{10}} \)
Das konnte ich dann durch die Lösungen so ausrechnen, aber ich weiß nicht wie man auf die 1.85 kommt.
Das Vertrauensintervall ist [0,313;0,832]
Vielen Dank für eure Antworten:)