Durchlaufen einer Pfeilkette

Question

Aufgabe:Beim Durchlaufen einer Pfeilkette liest man $+\vec{a}$ in Richtung der Spitze, $-\vec{a}$ gegen die Richtung der Spitze ab, also in der Figur $\vec{a}=\vec{d}-\vec{c}+\vec{b} \quad$ oder $\quad-\vec{a}=-\vec{b}+\vec{c}-\vec{d}$
Beschreibe ebenso $\overrightarrow{\mathrm{b}}$ bzw. $\overrightarrow{\mathrm{c}}$ bzw. $\overrightarrow{\mathrm{d}}$ mithilfe der anderen Vektoren.

Problem/Ansatz: Hallo

Es wäre nett wenn jemand mir helfen könnte.

Bitte Rechnung mit Lösung bin verzweifelt.

Answer 1

$\vec{d}$ =$\vec{a}$ -$\vec{b}$ +$\vec{c}$

$\vec{c}$ =$\vec{b}$ -$\vec{a}$ +$\vec{d}$

$\vec{b}$ =$\vec{c}$ -$\vec{d}$ +$\vec{a}$

Answer 2

Hallo,

schau dir doch mal genau das Beispiel an:

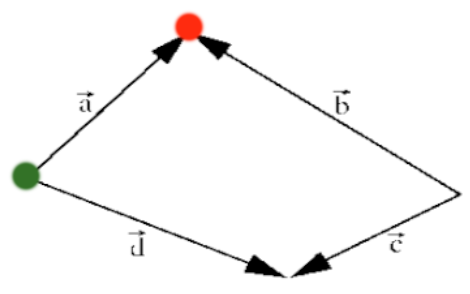
die Möglichkeiten von grün nach rot zu kommen sind

$\vec{a}$ oder den "Umweg außen rum"

$\vec{d}$ - $\vec{c}$ +$\vec{b}$

minus vor $\vec{c}$, weil wir umgekehrt zur Pfeilrichtung gehen

$\quad-\vec{a}=-\vec{b}+\vec{c}-\vec{d}$ ist dann der Weg von rot nach grün

Hast du das verstanden?

Gruß, Silvia

Answer 3

$$a=b-c+d$$$$b=a+c-d$$$$c=-a+b+d$$$$d=a-b+c$$