Text erkannt:
Fig. 1. Stellen Sie mithilfe einer Linearkomhination der Vektoren \( \overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \) und \( \overrightarrow{\mathrm{c}} \)
a) den Vektor \( \overrightarrow{\mathrm{AG}} \)
b) den Vektor \( \overrightarrow{\mathrm{BH}} \),
c) den Vektor \( \overrightarrow{\mathrm{EC}} \)
d) den Vektor \( \overrightarrow{\mathrm{BM}} \)
e) den Vektor \( \overrightarrow{\mathrm{ME}} \) dar.
13 In jedem Dreieck schneiden sich die Verbindungsstrecken der Eckpunkte mit den orrec
Aufgabe 12 bitte
Verstehe das nicht
Text erkannt:
\( 6,3 \vec{a}+7,4 \vec{b}-2,8 \vec{c}+17,5 \vec{a}-9,3 \vec{c}+\vec{b}-\vec{a}+\vec{c} \)
f) \( 3 \cdot(\vec{a}+2 \cdot(\vec{a}+\vec{b})) \)
g) \( 6 \cdot(\vec{a}-\vec{b})+4 \)
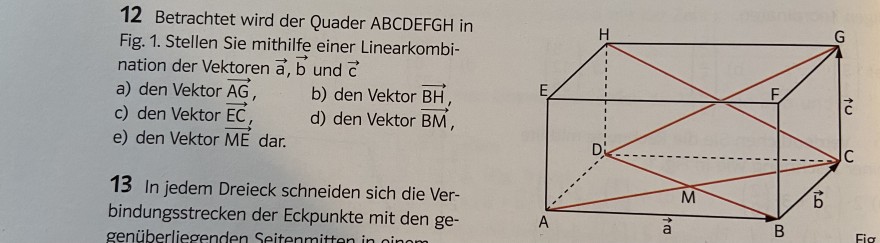
12 Betrachtet wird der Quader ABCDEFGH in Fig. 1. Stellen Sie mithilfe einer Linearkombination der Vektoren \( \overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \) und \( \overrightarrow{\mathrm{c}} \)
a) den Vektor \( \overrightarrow{\mathrm{AG}} \)
b) den Vektor \( \overrightarrow{\mathrm{BH}} \)
c) den Vektor \( \overrightarrow{\mathrm{EC}} \),
d) den Vektor \( \overrightarrow{\mathrm{BM}} \),
e) den Vektor \( \overrightarrow{\mathrm{ME}} \) dar.
13 In jedem Dreieck schneiden sich die Verbindungsstrecken der Eckpunkte mit den gegenüberliegenden Seitenmitten