Funktion in Polynom und echt gebrochen-rationalen Anteil zerlegen

Question

Aufgabenstellung:

Zerlegen Sie den Funktionsterm von f in eine Summe aus einem Polynom und einem echt gebrochenen-rationalen Anteil.

Ansatz:

Funktionsterm: f(x) = 2x-5/x-3

Ich habe die Polynomdivision angewendet und folgendes raus: 2 + 1/x-3 , also als Asymptote 2 und als Rest 1/x-3. War das alles? Ist dies was verlangt wurde?

Danke

Answer 1

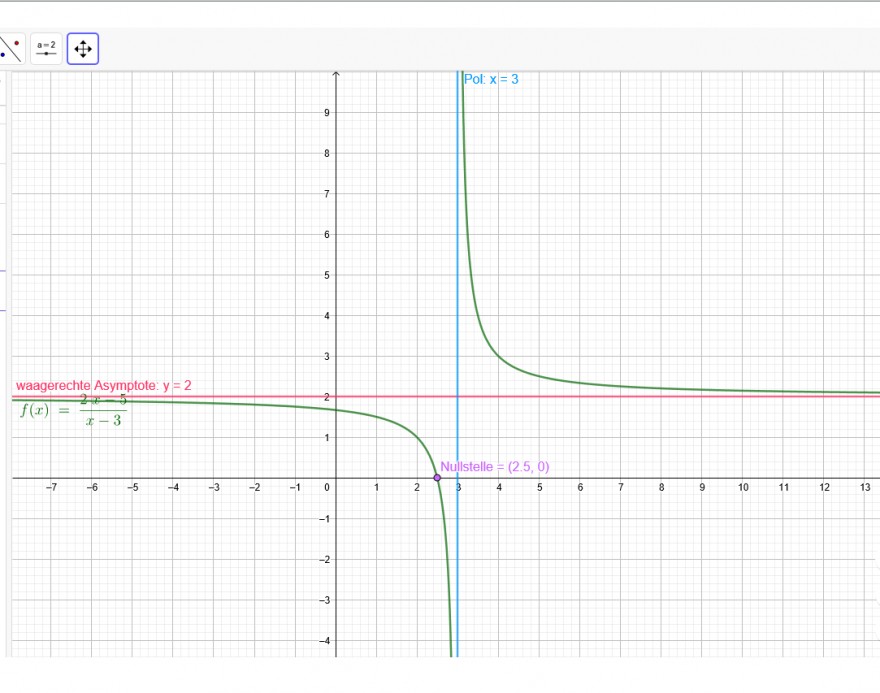
f(x) =  \( \frac{2 x - 5 }{ x - 3 } \)

Polynomdivision: ( führt zur Asymptote : hier ist die Asymptote waagerecht, es gibt noch andere Formen von Asymptoten)

(2 x - 5)  : ( x - 3 )  = 2 +  \( \frac{1 }{ x - 3 } \)

-(2  x - 6)

_____________

 0    +   1

Nullstelle: (Zähler des Bruches =0)

 2 x - 5  =  0     → x= 2,5   (Aber der Nenner des Bruches darf bei x=2,5 nicht auch 0 werden !)

Polstelle: (Nenner des Bruches = 0)

x - 3 = 0

x = 3

Comments

Besten Dank! ^^

Answer 2

Vielleicht so
p ( x ) = 2 * x^0
g ( x ) = 1 / ( x - 3 )

2 * x^0 + 1 / ( x - 3 )