Kann mir jemand zufällig helfen und diese Aufgabe lösen?
Beweisen Sie, dass die Menge
V : 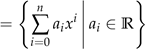
Text erkannt:
\( =\left\{\sum \limits_{i=0}^{n} a_{i} x^{i} \mid a_{i} \in \mathbb{R}\right\} \)
Text erkannt:
\( =\left\{\sum \limits_{i=0}^{n} a_{i} x^{i} \mid a_{i} \in \mathbb{R}\right\} \)
Text erkannt:
\( =\left\{\sum \limits_{i=0}^{n} a_{i} x^{i} \mid a_{i} \in \mathbb{R}\right\} \)
für festes n∈N mit den folgenden Verknüpfungen ein Vektorraum ist.
$$( \sum\limits{i=0}^{n}{a{i}x^{i} + \sum \limits{i=0}^{n} b{i}x^{i} := \sum \limits{i=0}^{n}(a{i}}+b_{i})x^{i} ) $$
$$ λ \sum \limits{i=0}^{n}a{i}x^{i} := \sum \limits{i=0}^{n}λa{i}x^{i} $$
(V heißt Vektorraum der Polynome vom Grad kleiner gleich n.)