Ich schreibe es mal mit = auf.
2x² = x - a
2 x² - x = - a
x^2 - \( \frac{x}{2} \) = - \( \frac{a}{2} \)
(x- \( \frac{1}{4} \)) ^2 = - \( \frac{a}{2}\) + \( \frac{1}{16}\) = \( \frac{1- 8a}{16} \)
(x- \( \frac{1}{4} \)) ^2 = \( \frac{1- 8a}{16} \)
x₁ = \( \frac{1}{4} \) +( \( \frac{1- 8a}{16} \) ) ^ \( \frac{1}{2} \)
x₂ = \( \frac{1}{4} \) - ( \( \frac{1- 8a}{16} \) ) ^ \( \frac{1}{2} \)
\( \frac{1- 8a}{16} \) = 0
a = \( \frac{1}{8} \)
Bei a=1/8 berührt die Parabel die Gerade.
Bei a<1/8 gibt es 2 Schnittpunkte.
Bei a>1/8 gibt es keinen Schnittpunkt.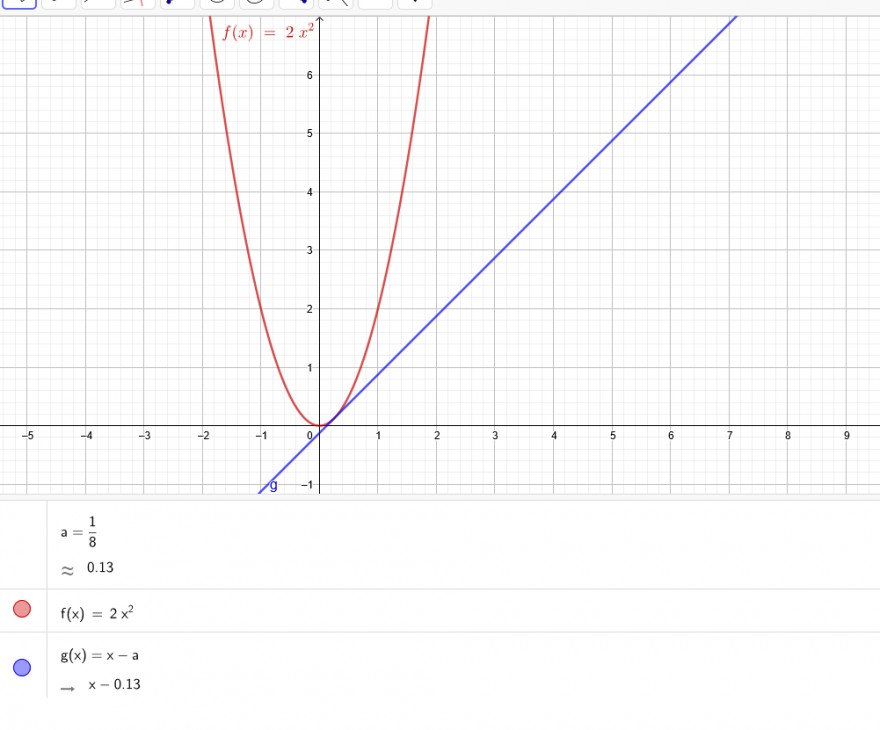
Text erkannt:
\( \mathrm{a}=\frac{1}{8} \)
\( \approx 0.13 \)
\( f(x)=2 x^{2} \)
\( g(x)=x-a \)
\( x-0.13 \)