Multiplikatives Gleichungssystem lösen?

Question

Aufgabe:

Ich habe Probleme beim Lösen dieses GLS.

1) 625 = a * 1,8^-b

2) 5000 = a * 0,9^-b

Problem/Ansatz:

Ich kenne die Lösung des Gleichungssystems. Weiß aber nicht wie man darauf gekommen ist..

Comments

Teile 1) durch 2)

a fällt raus und du erhältst b.

Answer 1

Da setzen wir ein

\(\small 625 = 5000 \; \left(\frac{9}{10} \right)^{b} \; \left(\frac{9}{5} \right)^{-b}\)

fassen zusammen

\(\small 625 = 5000 \; \left(\frac{9}{10} \cdot \frac{5}{9} \right)^{b}\)

und erhalten

\(\small 2^{b} = \frac{5000}{625}\)

Rest bekannt?

Answer 2

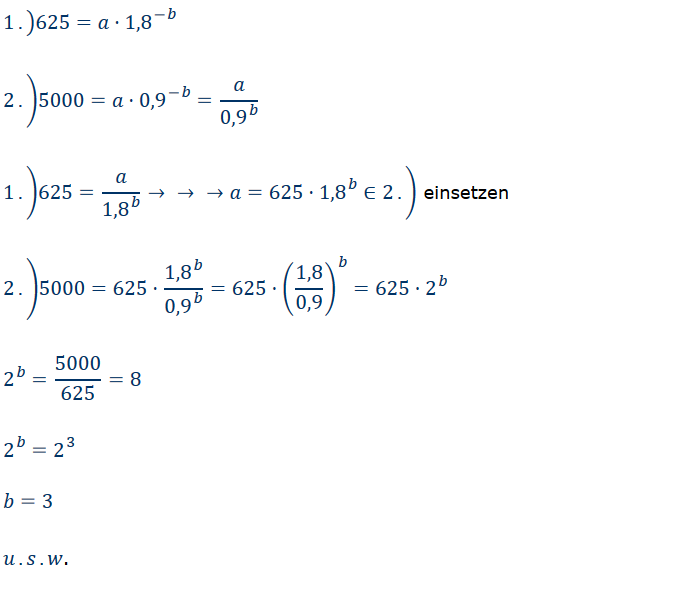
Text erkannt:

1.) \( 625=a \cdot 1,8^{-b} \)
2. \( ) 5000=a \cdot 0,9^{-b}=\frac{a}{0,9^{b}} \)
1.) \( \left.625=\frac{a}{1,8^{b}} \rightarrow \rightarrow \rightarrow a=625 \cdot 1,8^{b} \in 2 .\right) \) einsetzen
2. \( ) 5000=625 \cdot \frac{1,8^{b}}{0,9^{b}}=625 \cdot\left(\frac{1,8}{0,9}\right)^{b}=625 \cdot 2^{b} \)
\( 2^{b}=\frac{5000}{625}=8 \)
\( 2^{b}=2^{3} \)
\( b=3 \)

Comments

Sehr vielen Dank!