Rationale Funktionen berechnen

Question

Aufgabe:

Untersuchen Sie die Funktion f(x)=1/4x+1/x , x≠0 und g(x)=x^4-2x^2 auf Nullstellen, Extrema und Wendepunkte. Skizzieren Sie die Graphen von f und g.

Problem/Ansatz:

Brauche wirklich Hilfe, Danke

Answer 1

Keine Nullstellen und keine Wendepunkte.

f '(x)=1/4-1/x² Extrema bei x=2 und x= - 2.

Answer 2

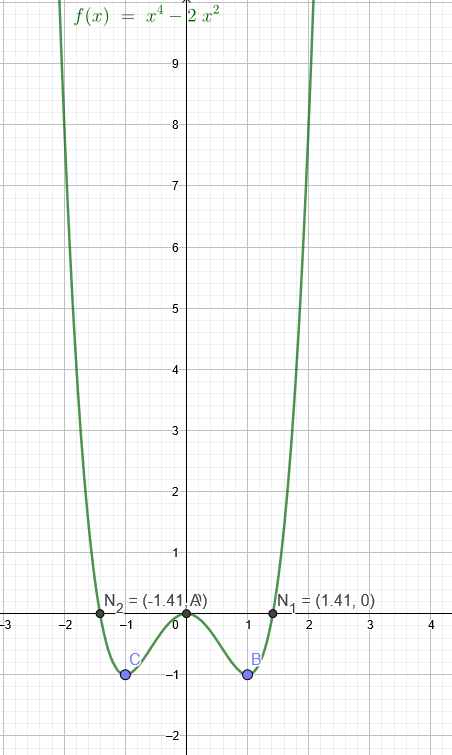
g(x)= x^4  - 2x^2

Nullstellen:  g (x)=0

x^4  - 2 x^2=0

x^2 •  ( x^2 - 2 )=0

x^2=0  ist eine doppelte Nullstelle

(x^2 - 2 )  =0

x^2 =  2

x_3 =    \( \sqrt{2} \)

x_4 =  -\( \sqrt{2} \)

Extrema: g ´ (x) = 0

g´(x)=   4 • x^3  - 4x

4 • x^3  - 4 x = 0

x^3  -  x = 0

x•( x^2-1) = 0

x_1 = 0  → g(x_1)=...

x_2 = 1 → g(x_2)=...

x_3 =  - 1 → g(x_3)=...

Art der Extrema:

g´´(x) = 12 x^2 -  4

g´´(0) =  - 4  <  0  →  Maximum

g´´(1) = 12  - 4= 8 > 0 →  Minimum

g´´(-1) = 12  - 4= 8 > 0 → Minimum

Wendepunkte : g´´ (x)  =  0

12 x^2 - 4= 0

x^2 = \( \frac{1}{3} \)

x_1=... →   g(x_1)=  ...

x_2=... → g(x_2)=  ...