Aufgabe:
Beweisen Sie unter Nutzung des Satzes von Thales und des Umfangwinkelsatzes die
folgende Aussage:
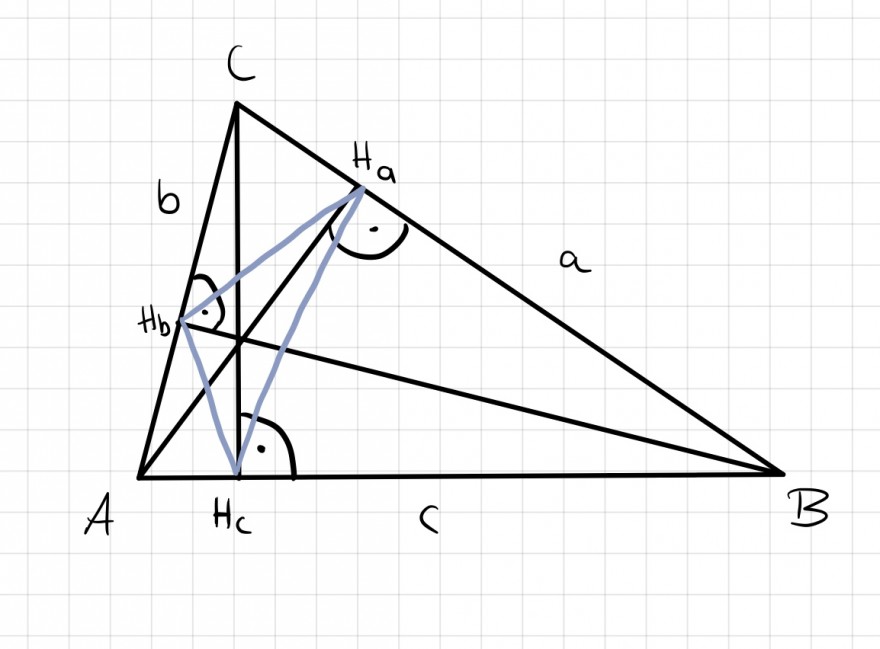
Die Höhen eines Dreiecks sind die Winkelhalbierenden des Dreiecks, das man erhält,
wenn man alle drei Höhenfußpunkte (Schnittpunkte der Höhen mit der zugehörigen
Dreiecksseite) zu einem Dreieck verbindet.
(Der Umfangwinkelsatz lautet: Seien A und B zwei verschiedene Punkte der Ebene. Durch jeden Punkt P außerhalb von AB kann der
Umkreis des Dreiecks ABP konstruiert werden. Sei M der Mittelpunkt dieses Kreises.
Dann ist der Umfangswinkel ∢(APB) halb so groß wie der Mittelpunktswinkel ∢(AMB), den die Radien
AM und BM auf dem P abgewandten Teil des Kreises einschließen.)
Problem/Ansatz:
Ich habe mir eine Skizze gemacht, komme aber leider auch hier nicht weiter, da ich nicht weiß, wo ich anfangen soll, an welcher Stelle ich die Sätze anwenden sollte o.ä.
Ich würde mich über eine Anregung für den Start freuen.