Dreieck konstruieren mit c = 7 , γ = 56° und dem Inkreisradius p = 2 (S sei der Mittelpunkt des Inkreises)

Question

Dreieck konstruieren mit c = 7 , γ = 56° und dem Inkreisradius p = 2 (S sei der Mittelpunkt des Inkreises)

Aufgabe:

Konstruieren Sie ein Dreieck mithilfe der folgenden Angaben c = 7cm, γ = 56° und dem Inkreisradius p = 2cm (S sei der Mittelpunkt des Inkreises).
Hinweis: Weisen Sie zuerst nach, dass ∢(ASB) = 90° + 1/2 beträgt.

Problem/Ansatz:

Zuerst sollen wir ja nachweisen, dass ∢(ASB) = 90° + 1/2 . Hier scheitere ich allerdings schon.. Wie kann ich das denn zeigen?

Ich habe es geschafft zu zeigen, dass in diesem Fall ∢(ASB) = 118° gilt. Allerdings bekomme ich es nicht hin, dies allgemein zu zeigen.

Leider weiß ich auch nicht, wie ich dann am besten mit der Konstruktion weitermachen soll.

(Ich weiß, dass S der Schnittpunkt der Winkelhalbierenden sein muss und dass die Winkelhalbierenden durch S im Verhältnis 1:2 geteilt werden)

Ich freue mich über jede Hilfe!

Text erkannt:

(2)

Gefragt 28 Jan 2021 von mariexbee

"(Ich weiß, dass S der Schnittpunkt der Winkelhalbierenden sein muss und dass die Winkelhalbierenden durch S im Verhältnis 1:2 geteilt werden)"

S ist der Schwerpunkt eines Dreiecks. Ihn findest du nicht mit den Winkelhalbierenden.

Hierzu müssen die Seiten halbiert werden und dann mit der gegenüberliegenden Ecke verbunden werden.

Das sind ja dann mal zwei Fehlschläge auf engstem Raum.

@mariexbee

Die Winkelhalbierenden teilen sich im Allgemeinen nicht im Verhältnis 2:1.

@Moliets

mariexbee kann immerhin lesen. Sie hat im Gegensatz zu dir die Passage

(S sei der Mittelpunkt des Inkreises).

im Aufgabentext entziffern können. Wie kommst du zu der hirnrissigen Annahme, das ein Punkt nur deshalb Schwerpunkt eines Dreiecks sein sollte, weil der Aufgabensteller ihm den lustigen Namen "S" gegeben hat?

Solches Schablonendenken kann ich meinen Schülern durch wiederholte gegenteilige Aufgabenstellungen sukzessive austreiben.

Dass aber eifrige Antwortgeber solchen Bockmist verzapfen ist verwerflich.

Kommentiert 28 Jan 2021 von abakus

📘 Siehe "Dreieck" im Wiki

3 Antworten

Beste Antwort

Hinweis: Weisen Sie zuerst nach, dass ∢(ASB) = 90° + 1/2 beträgt.

Das soll vermutlich ∢(ASB) = 90° + 1/2 γ heißen.

Ich habe es geschafft zu zeigen, dass in diesem Fall ∢(ASB) = 118° gilt.

Also besitzt das Teil-Dreieck ASB einen Umkreis, auf dem der Peripheriewinkel ∢(ASB) eine Größe von 118° hat. (Der zugehörige Zentriwinkel ist dann 236°.)

Konstruiere die Strecke AB=c=7cm und einen Punkt X, für den ∢(AXB) = 118° gilt.

Konstruieren den Umkreis von AXB, auf dem muss auch S liegen.

Konstruieren Sie ein Dreieck mit ... und dem Inkreisradius p = 2cm

Dann hat S von AB den Abstand 2 cm.

Eine Parallele zu AB (auf der richtigen Seite von AB schneidet den Umkreis von AXB. Einer der beiden entstehenden Schnittpunkte ist S.

Damit solltest du weiterkommen.

Beantwortet 28 Jan 2021 von abakus

Ein anderes Problem?

Stell deine Frage

mathef · Answer 1 · 2021-01-28T18:26:16+0000

Die Winkelhalbierenden werden nicht im

Verhältnis 1:2 geteilt. Das hast du mit den Seitenhalbierenden

verwechselt.

Im Dreieck ASB hast du bei A den Innenwinkel α/2 und Bei B dann ß/2

also ist Winkel ASB = 180° - ( α/2 + ß/2 ) = 180° - ( α+ß)/2

= 180° - ( 180°-γ)/2 = 90° + γ/2

Werner-Salomon · Answer 2 · 2021-01-29T10:31:37+0000

Hallo,

Weisen Sie zuerst nach, dass ∢(ASB) = 90° + 1/2 beträgt.

zeige ich später, ist aber für die Aufgabe nicht notwendig! IMHO eleganter ist es mit der Kenntnis des Südpolsatzes vorzugehen.

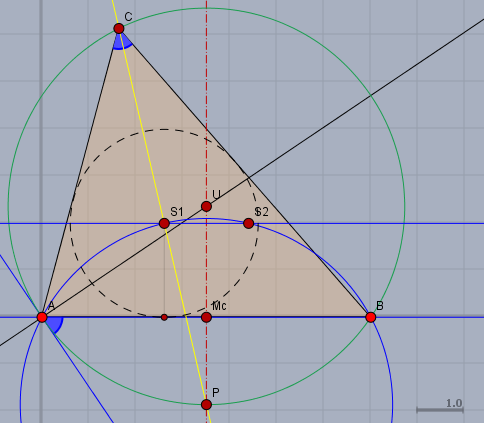
Zeichen die Strecke $AB$ und ihre Mittelsenkrechte (rot Strich-Punkt). Dann trage den Winkel $\gamma = 56°$ (blau) unterhalb der Strecke $AB$ in $A$ ab. Das Lot (schwarz) durch $A$ auf dem Schenkel (blau) von $\gamma$ schneidet die Mittelsenkrechte in $U$. $U$ ist der Mittelpunkt des Umkreises (grün), der die Mittelsenkrechte unterhalb von $AB$ in $P$ schneidet. Schlage einen Kreis (blau) um $P$ mit Radius $PA$.

Konstruiere die Parallele zu $AB$ oberhalb von $AB$ im Abstand von $p=2\,\text{cm}$. Diese Parallele schneidet den Kreis um $P$ in den Punkten $S_1$ und $S_2$. Die Gerade durch $P$ und $S_1$ schneidet den Umkreis in $C$. Das Dreieck $\triangle ABC$ ist das gesuchte Dreieck. Die Gerade durch $P$ und $S_2$ liefert ein zur Mittelsenkrechte symmetrisches Dreieck.

Beweis, dass $\angle ASB = 90° + \frac 12 \gamma$:

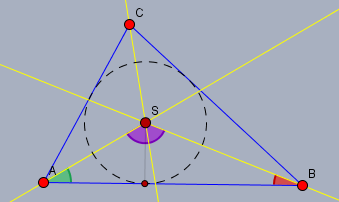
Die Winkelsumme im Dreieck $\triangle ABC$ ist $\alpha + \beta + \gamma = 180°$. Daraus folgt$$\begin{aligned} \alpha + \beta &= 180° - \gamma \\ \frac 12 \alpha + \frac 12 \beta &= 90° - \frac 12 \gamma\end{aligned}$$Im Dreieck $\triangle ABS$ ist$$\frac 12 \alpha + \frac 12 \beta + \angle ASB = 180° \\ \begin{aligned}\implies \triangle ASB &= 180° - \left( \frac 12 \alpha + \frac 12 \beta\right) \\&= 180° - \left(90° - \frac 12 \gamma\right) \\&= 90° + \frac 12 \gamma\end{aligned}$$Gruß Werner

Dreieck konstruieren mit c = 7 , γ = 56° und dem Inkreisradius p = 2 (S sei der Mittelpunkt des Inkreises)

3 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: