Aufgabe:
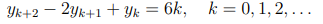
Text erkannt:
\( y_{k+2}-2 y_{k+1}+y_{k}=6 k, \quad k=0,1,2, \ldots \)
Meine Lösung:
1. Lösung der homogenen Gleichung:
Das charakteristische Polynom: \( q^{2} -2q +1 = 0 => q= 1 \)
Die allg. Lösung :
\( y_{k,hom} = c_{1} + c_{2}k \)
2. Partikuläre Lösung der inhomogenen Differenzengleichung:
\( y_{k+2}-2 y_{k+1}+y_{k}=6k\)
Lösungsansatz \(y_{k} = A_{0} + A_ {1}k \) Einsetzen in die Gleichung:
\( A_{0} + A_ {1} (k+2) - 2(A_{0} + A_ {1} (k+1)) + A_{0} + A_ {1}k = 6k \)
\( 0 = 6k \)
Danach kann ich leider nicht weiter machen. Ich weiß nicht, wo ist den Fehler.