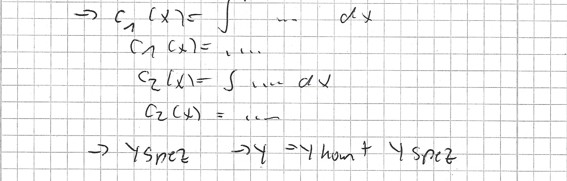Wie kann man dieses inhomogenes DGL System 1.Ordnung lösen?

Question

Aufgabe:

Hallo an alle ich hab ein Problem beim Lösen eines inhomogenen DGL Systems 1.Ordnung

Text erkannt:

\( \left(\begin{array}{l} y_{1}^{\prime}(x) \\ y_{2}^{\prime}(x) \end{array}\right)=\left(\begin{array}{cc} 3 x-1 & x-1 \\ -x-2 & x-2 \end{array}\right)\left(\begin{array}{l} y_{1}(x) \\ y_{2}(x) \end{array}\right)+\left(\begin{array}{c} x \\ -\frac{1}{2} \end{array}\right) e^{x^{2}} . \)
Weiterhin seien mit
\( \vec{y}^{(1)}(x)=\frac{1}{3}\left(\begin{array}{c} 1 \\ -1 \end{array}\right) e^{x^{2}} \quad \text { und } \quad \vec{y}^{(2)}(x)=\left(\begin{array}{l} 2-3 x \\ 7+3 x \end{array}\right) e^{x^{2}-3 x} \)
zwei linear unabhängige Lösungen des zugehörigen homogenen Systems gegeben.

Problem/Ansatz:

Also normalerweise würde man ja die Eigenvektoren berechnen, dann die homogene Lösung und dann die Partikulärlösung. und zuletzt die allg. Lösung

Ich bin verwirrt wegen den x`en im System und weiß auch nicht wie ich jetzt weitermachen soll. Kann mir jemand helfen?

Answer 1

Hallo,

"Also normalerweise würde man ja die Eigenvektoren berechnen, dann die homogene Lösung und dann die Partikulärlösung. und zuletzt die allg. Lösung
Ich bin verwirrt wegen den x`en "--------->das Verfahren mit den Eigenwerten, Eigenvektoren funktioniert hier nicht, weil es keine Konstanten sind.

Die homogene Lösung brauchst Du nicht mehr berechnen, ist gegeben.

(y1(x) und y2(x)). Die Lösung erfolgt durch Variation der Konstanten.

Ich habe den Weg allgemein geschrieben .(falls in der Vorlesung behandelt)

det(A)=  \( \frac{1}{3} e^{(x-3) x}\left(9 x+e^{3 x}+21\right) \)

Comments

Vielen Dank, es hat mir sehr geholfen