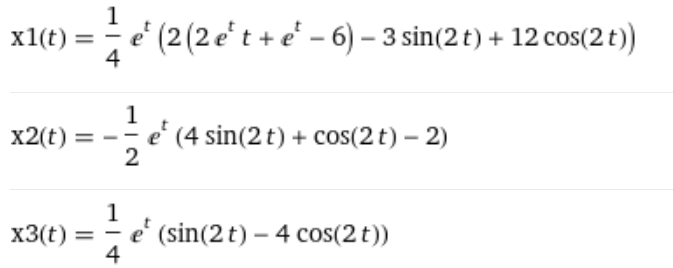Hallo,
Hier der Weg über die Eigenwerte und Eigenvektoren und dem Ansatz über die rechte Seite.
Es gibt auch noch andere Möglichkeiten.
Ich habe folgendes erhalten:
1.Eigenwerte: (z.B über die Regel von Sarrus)
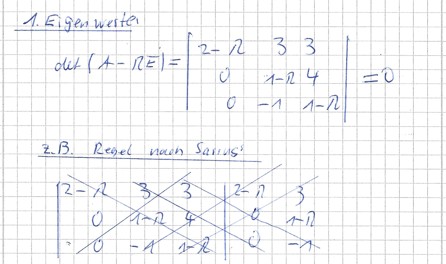
\( \begin{array}{l}(2-\lambda)(1-\lambda)(1-\lambda)+0+0-[0-8+4 \lambda+0]=0 \\ (2-\lambda)(1-\lambda)^{2}+8-4 \lambda=0 \\ (2-\lambda)\left(1-2 \lambda+\lambda^{2}\right)+8-4 \lambda=0\end{array} \)
\( \begin{array}{l}2-4 \lambda+2 \lambda^{2}-\lambda+2 \lambda^{2}-\lambda^{3}+8-4 \lambda=0 \\ -\lambda^{3}+4 \lambda^{2}-9\lambda+10=0 \quad \text |(-1) \\ \lambda^{3}-4 \lambda^{2}+9 \lambda-10=0 \\ (\lambda-2)\left(\lambda^{2}-2 \lambda+5\right)=0 \\ \lambda_{1}=2 ; \lambda_{{2}_{3}}=1 \pm 2 i \\\end{array} \)
2.Eigenvektoren:
\( v_{1}=(-3,-2 i, 1) \)
\( v_{2}=(-3,2 i, 1) \)
\( v_{3}=(1,0,0) \)
->homogene Lösung:
\( x=C_{1} e^{2 t}\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)+C_{2} e^{t}\left(\cos (2 t)\left(\begin{array}{c}-3 \\ 0 \\ 1\end{array}\right)-\sin (2 t)\left(\begin{array}{c}0 \\ -2 \\ 0\end{array}\right)\right)+C_{3} e^{t}\left(\cos (2 t)\left(\begin{array}{c}0 \\ -2 \\ 0\end{array}\right)+\sin (2 t)\left(\begin{array}{c}-3 \\ 0 \\ 1\end{array}\right)\right) \)
weiterer Weg:
Ansatz der part. Lösung: (Einsetzen von xp1 , xp1' ,xp2 , xp2',xp3 , xp3' in die Aufgabe):
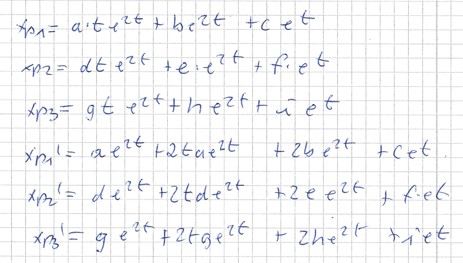
--> Koeffizientenvergleich:

Lösung des Gleichungssystems führt zu:
xp1= t \( e^{2t} \) -3 \( e^{t} \)
xp2= \( e^{t} \)
xp3=0
x=xh+xp
Einsetzen der AWB in die Lösung:

Kontrolle Wolfram alpha: